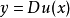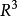蒙日一安培方程

蒙日一安培方程是一類從黎曼幾何問題中提出來的二階完全非線性偏微分方程，同時也是卡拉比-丘流形證明時曾用的工具。蒙日一安培方程由於其完全非線性的特性使得其求解一直是一個困難的問題。蒙日一安培方程的套用十分廣泛，在微分幾何、變分法、最最佳化問題及傳輸問題等領域均有套用。

基本介紹

• 中文名：蒙日一安培方程
• 外文名：Monge-Ampere equation
• 所屬學科：二階完全非線性偏微分方程
• 方程類型：完全非線性橢圓型
• 提出者：蒙日、安培
• 套用領域：微分幾何變分法最最佳化及傳輸問題

數學表示

定義兩個非獨立變數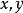，以及一個獨立變數，蒙日-安培方程可以表述為：

這裡的為一階變數，是唯一的非獨立函式。

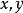
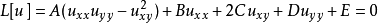
Rellich定理

是一個的有界區域，在上是關於的連續函式，蒙日-安培方程的狄利克雷問題可以表示為：

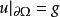
如果有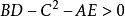，那么這個狄利克雷問題至多兩個解。

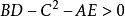
橢圓型蒙日-安培方程

如果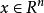，且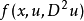是一個正值函式，那么蒙日-安培方程：

是一個完全非線性橢圓型偏微分方程。

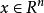
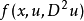
套用

該方程在微分幾何、變分法、最最佳化問題及傳輸問題等領域有廣泛套用。在通過圖像的匹配進行搜尋時，輸入一個圖像，在網上尋找最相近的圖像。黑白照片由灰黑色點組成，可以看成是一個機率分布：該點的顏色越黑，就認為該點的機率密度越大。於是兩張照片匹配問題就轉化為兩個機率分布的匹配問題。1991年，白羅尼發現，如果這兩個分布都是連續分布，那么這個匹配對應的可以寫成一個梯度映射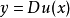，其中是一個凸函式，且滿足著名的蒙日-安培方程。