菲力浦斯\x22SSS\x22標準

菲力浦斯"SSS"標準全名為菲力浦斯標準抽樣體系，是一種抽樣方法，在歐洲套用比較廣泛。其特點是確定抽樣特性曲線上的控制點，即L(P_0.5)=1/2，與此點的相對斜率h₀可以確定唯一的一條OC曲線，如果改變一次抽樣方案的樣本大小n，而接收數c保持不變，特性曲線只根據p軸的尺度而變，而其他方面保持不變。同樣改變二次抽樣方案的n₁/n₂之值，而c₁,c₂和c₃保持不變也有同樣的結果。這種轉換不改h₀值。即h₀是獨立於樣本或樣本組大小的絕對值。因此要調整任何抽樣方案到事先規定的控制點，只要簡單地通過改變樣本或樣本組的大小。

基本介紹

• 中文名：菲力浦斯"SSS"標準
• 外文名：Phillips "SSS" standard
• 全名：菲力浦斯標準抽樣體系
• 屬性：一種抽樣方法
• 方案：一次抽樣和二次抽樣方案

理論基礎

從幾何角度研究抽查特性曲線，可以發現它有兩個重要的特點，即曲線傾斜最大的位置和在這一點傾斜的程度，對各種抽樣方案的對應的抽查特性曲線上是有所差別的。可以用這兩個特點作為定義兩個參數的基礎，用它們來確定抽樣方案。

定義的第一個參數叫做控制點，在某些質量管理文獻中也叫做不偏點，可以用它來規定特性曲線的位置。所謂控制點就是一個不合格品率P_0.50，其對應接收機率為0.50，定義公式為L(P_0.5)=1/2，將以此點的相對斜率h₀來刻畫曲線在這點的傾斜程度。定義公式為圖1中的公式。

圖1 相對斜率定義公式

加上負號是為了使h₀經常保持正值。這裡以相對斜率代替絕對斜率（dL(p)/dp）_p=p0.50是有原因的。泊松分布機率是依賴於n和p之積np，而不是單獨的依賴於n和p。其結果，改變一次抽樣方案的樣本大小n，而接收數c保持不變，特性曲線只根據p軸的尺度而變，其他方面保持不變。同樣改變二次抽樣方案的n₁/n₂之值，而c₁,c₂和c₃保持不變也有同樣的結果。這種轉換不改h₀值。即h₀是獨立於樣本或樣本組大小的絕對值。

由於上面的特點，要調整任何抽樣方案到事先規定的控制點，只是簡單地通過改變樣本或樣本組大小。這種調整是容易進行的，因此，我們研究過的同一接收數的所有的一次抽樣方案，或者同樣判定數組和同樣樣本大小比例的二次抽樣方案都屬於一類。這類方案可以用一條抽查特性曲線來代表，它的主要特點只由一個參數h₀來刻畫。屬於一類抽樣方案的特性曲線，可以通過簡單和方便的方法合併成一條曲線，就是接收機率L(p)不是相對於不合格品率坐標，而是相對於p/p_0.50坐標而繪製的。

一次抽樣方案

樣本大小n與接收數c和P_0.50與h₀之間的關係，可以通過圖2 的經驗公式來確定。

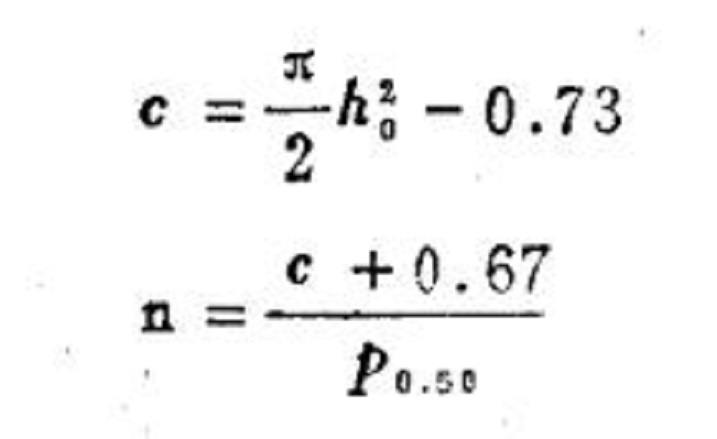
圖2經驗公式

按照菲力浦斯公司的規定，P_0.50在物理意義上，可以解釋為“好”批與“壞"批的分界線。因為這樣把質量區域一分為二地劃為“好”與“壞”兩個區域而無過渡區域(或不明確區域)，所以根據菲力浦斯公司的經驗，這種解釋是比較容易被生產方和使用方接收的。對於任何給定的P_0.50，利用上面公式容易計算所要求的一次抽樣方案。在計算抽樣方案方面，SSS標準體系比前面所介紹的標準型抽樣體系優越得多。

二次抽樣方案

二次抽樣方案比一次抽樣方案使用起來要複雜一些，只有在二次方案比一次方案優越的時候，才會使用二次方案。為了設計出比一次方案優越的二次方案，首先要解決兩種抽樣方式(一次抽樣和二次抽樣)如何比較的問題。