莫諾方程式是描述微生物比增殖速度與有機底物濃度之間的函式關係。法國生物學家Monod是研究低底物微生物學的專家，他於1942年和1950年前後兩次進行了單一底物的細菌培養試驗，結果表明微生物增殖速率是微生物濃度的函式，也是底物濃度的函式，提出與米-門關係類似的表示微生物比增殖速率與底物濃度的動力學關係式，即Monod方程式。
基本介紹
- 中文名：莫諾方程
- 外文名：Monod Equation
- 學科：生物學、生物反應動力學
- 套用：污水生物處理
內容,推論,求法,區別,套用,
內容
營養物質(底物)的濃度與組成影響微生物培養的生長速度，對微生物的生長起到限制作用的營養物即所謂的限制性底物。1942年，莫諾用純種的微生物在單一底物的培養基上進行了微生物增殖速度與底物濃度之間關係的試驗，試驗結果得出了如下圖所示的曲線，這個結果與米凱利斯-門坦(Michaelis-Menten)於1913年通過試驗所取得的酶促反應速度與底物濃度之間關係(米-門方程)的結果是相同的。因此，莫諾認為可以通過經典的米-門方程式來描述微生物比生長速度與單一限制性底物存在的關係，即莫諾(Monod)方程，見下式。
式中，
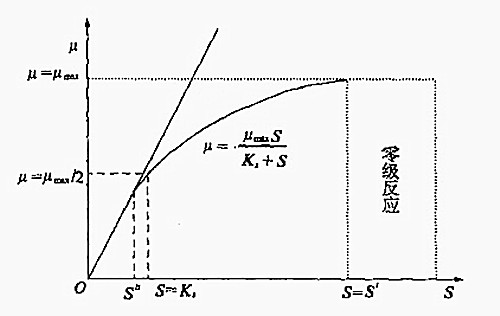比增長速率（μ）與底物濃度（S）的關係曲線推論
莫諾方程式是描述微生物比增殖速度與有機底物濃度之間的函式關係對這種函式關係在兩種極限條件下進行推論，能夠得出兩點結論。
①在高底物濃度的條件下，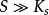
，方程中的
值可以忽略不計，於是方程可簡化為
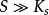
說明在高濃度有機底物的條件下，微生物以最大的速度增長，增長速度與有機底物的濃度無關，呈零級反應，即上圖所表示的底物濃度，S大於S'的區段。這時，有機底物的濃度再行提高，降解速度也不會提高，因為微生物處於對數增殖期，其酶系統的活性位置都被有機底物飽和。
②在低底物濃度的條件下，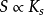
，在方程分母中S值可忽略不計，這樣方程可簡化為
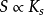
說明微生物增長遵循一級反應，有機底物的濃度已經成為微生物增長的控制因素，即上圖中底物濃度S=0~S"的區段，曲線的表現形式為通過原點的直線。這時，微生物酶系統多未被飽和，增加底物濃度將提高微生物的比增長速度。
求法
在莫諾方程中，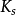
與
是兩個常數。它們的意義在於，這兩個常數隻與微生物種類及其底物有關，而與底物濃度無關，如表1所示。當微生物的種類和底物確定以後，
與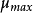
可以視為兩個不變的常數。因此，這兩個常數可以體現出微生物增長的特性，以及底物被微生物利用的特性。
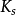
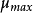
表1 影響Ks與μmax的兩個因素
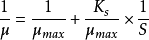
繪製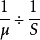
曲線，為一條直線，直線截距為
，斜率為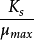
，可計算出
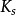與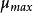
。
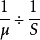
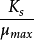
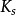
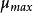
上述方法在底物濃度較低的情況下，誤差較大。在低濃度底物時可採用下式
繪製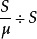
曲線，為一條直線，直線截距為
，斜率為
。
區別
雖然，莫諾方程與米-門方程的形式相同，但它們表達的意思完全不同，二者的區別如表2所示。
表2 莫諾方程與米-門方程比較套用
莫諾方程式是通過單一底物的純菌種培養實驗而得出的，而活性污泥處理系統的微生物是多種微生物群體，污水中的有機底物也是多種類的。20世紀60~70年代，勞倫斯(Lawrence)等人將莫諾方程式引入污水生物處理領域，推導出一系列公式，套用於污水處理廠設計，證實它是完全適用的。
