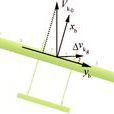
荷蘭滾是指當升力大於重力的時候,有規律的大幅度搖擺機翼,從後面看飛機就像鐘擺一樣,從上面看就是蛇行路線的現象。
基本介紹
- 中文名:荷蘭滾
- 類似:簡諧振動
- 特點:規律性強
- 意義:只用於測試,實戰意義不大
簡介,滾動特性,無人機滾動研究,
簡介
用教科書上的話就是飛機的橫滾穩定性強於偏航穩定性時飛機就會做荷蘭滾,而當飛機的偏航穩定性強於橫滾穩定性時飛機就會飛螺旋線,螺旋線的直徑不斷減小飛機就會最終進入螺旋。(常有人把這種機動和剪式機動混為一談,也有人把螺旋和尾旋混為一談,在此強調更正。)
 軸向滾轉運動示意圖
軸向滾轉運動示意圖荷蘭滾類似於簡諧振動,規律性強,實戰意義不大,只是用於測試;而剪式飛行則是左右頻繁交替的大攻角盤旋,通常是兩架相距很近的飛機同時做的動作,冒著撞機的危險不停的相互交叉,目的在於用機動性爭奪對方後面的有利位置,機動性好的最終獲勝。

滾動特性
飛機的動態特性(包括縱向和橫航向)是飛機操縱品質最重要的方面之一,所有的新型飛機及改型機都會重點檢查飛機此方面的特性,CCAR25部把它視為民用飛機具有穩定性的特性之一。試飛中對於動態特性的檢查通常是通過倍脈衝或倍階躍縱向和橫航向操縱裝置來激起飛機的縱向短周期特性和橫航向的荷蘭滾特性進行,通過數據處理得到飛機的動態特性的阻尼比ζ、無阻尼自振頻率ωn和阻尼ξ等,以檢查飛機動態特性是否滿足相應標準和規範的要求。
現代的飛機動態特性的飛行試驗通常採用最大似然法的參數辨識進行動特性指標的計算,但是由於該方法是以機率最大作為條件進行指標提取,對於具有較小阻尼比(ζ<0.3)的飛機來講,也許並不是一種較好的方法。在某型機的動特性參數辨識中,飛機荷蘭滾運動是明顯收斂的,但是辨識出來的阻尼比f甚至變成了負值,與實際結果很不一致。由此,需要一種精確地計算小阻尼比飛機動特性的方法。
由於各型飛機的動特性(包括阻尼比、振幅、周期等)有明顯差異,要想使程式適用於不同飛機,就必須設計一種算法,以便提取出該型機動特性所需要的門限值信息。我們可以取一固定時間視窗內的自由振動數據分析,該時間視窗長度設定為不大於幅值最大的波峰和波谷問的時間長度,恰好等於阻尼振動周期T的一半,給定測試數據及動作時間段信息,就可求出幅值最大的波峰和波谷間的時間長度。該時間視窗長度內的振動數據有以下特徵,對於包含波峰或波谷的時間長度,且波峰與波谷基本上位於該時間視窗中央時,該時間視窗兩端的數據基本相等。由於試飛測試數據是等採樣間隔的離散點,故可以從整個動作時間段內選取出所有離散點的最大增量Δx,用Δx作為該時間視窗兩端的數據基本相等的依據,那么就可以找出這么一個時間視窗,它的長度已經是求出來了,約等於阻尼振動周期T的一半。用兩端值的差小於Δx來判斷時間視窗是否成立,一旦找到它,就可以找出其中的波峰或波谷及對應的時間,然後將時間視窗兩端向後跳躍約1/4T,繼續用上述判據來尋找選取的動作時間段內的剩餘波峰及波谷,直至動作時間結束。
對於上面得到的所有波峰及波谷,還要進行一些相關的出錯檢查機制。比如用每一個波峰及波谷間的時間長度與總的平均波峰與波谷問的長度比值來判斷程式自動取點是否正確。另外還要檢查相鄰的頂點符號是否相反,通過出錯檢查機制,可以及時發現程式的智慧型取點是否正確,避免計算錯誤。
無人機滾動研究
無人機常替代有人機在危險環境中飛行,故障發生機率大,所以研究特定故障下的無人機運動特性,並對其進行有效控制,最終能步出不穩定飛行狀態是無人機研究的重要內容之一。
首先,深入分析單副翼卡死故障下無人機的受力情況,將單副翼卡死視為一個常值干擾,建立起故障後無人機的側向運動方程,並運用小擾動線性化得出無人機側向的線性化方程;其次,根據兩種不同操縱舵面對單副翼卡死所產生的影響給予補償,通過力矩平衡關係,得出單副翼有限卡死的範圍,以保證其餘舵面能夠給予有效的控制,使無人機能夠正常飛行;第三,套用經典PID控制方法對正常情況下無人機橫側向控制律進行設計及仿真驗證;最後,在正常控制律的基礎上,運用容錯控制中的偽逆法設計了步出荷蘭滾運動模態的控制律,並且通過仿真驗證所設計的控制律基本滿足要求。
重構飛行控制系統主要採用了主動容錯控制技術,首先對飛行控制系統的故障進行檢測和辨識,然後充分利用飛控系統的功能冗餘來進行飛控系統的控制律重構,使飛機能夠更好的適應更大範圍的故障及特殊的任務環境。從而使飛機在出現較嚴重的故障和戰鬥損傷的情況下,保持飛機自身的飛行性能,並且保證飛行員能夠順利完成任務或安全返航。
建立單副翼卡死時的故障模型有兩種方法:一是把單副翼卡死當作無人機自身的固有結構來處理,這就需要我們重新分析作用在無人機機身上的力及力矩關係,再列寫出單副翼卡死時的十二個一階微分方程,重新建立出力和力矩方程的關係式,從這一點來說,這種方法分析起來十分複雜,但它的優點是能夠更好地反映出無人機單副翼卡死時自身的運動特性;二是把卡死舵面當作一個常值干擾,此方法屬於靜態補償問題。
正常無人機的模型入手,深入分析了單副翼卡死所產生的力及力矩,然後把單副翼卡死所產生的力及力矩視為常值來列寫出兩種無人機飛控布局的故障模型,並且套用小擾動線性化原理對其故障模型進行線性化處理。