基本介紹
- 中文名:芝諾疑難
- 提出者:芝諾 Zenon Eleates
- 提出時間:約公元前490~約公元前436
簡介,兩分法,阿基里斯追不上烏龜,飛矢不動,運動場,
簡介
古希臘哲學家芝諾是一位很有趣的人物,他以提出“兩分法”、“阿基里斯追不上烏龜”、“飛矢不動”和“運動場”等疑難問題而聞名於世。本來這些疑難都是荒謬的,但是他提出的理由又是那樣的雄辯,仿佛無懈可擊,以致在19世紀之前,沒有任何人能駁倒他。以下是關於這四個疑難問題的介紹:
兩分法
“兩分法”是芝諾疑難中最有代表性的一個。芝諾認為,物體不能存在運動,即不可能從A點運動到B點。理由是,物體在到達B點之前必須通過AB的中點C。要到達C,又須先通過AC的中點D……依次類推,還有AD的中點E,AE的中點F……,無窮無盡。物體怎么能在有限的時間內通過無窮個點呢?這樣,物體就被無窮箇中點所阻隔,每箇中點都是一個障礙,由於無數箇中點,永遠無窮無盡,所以物體不能從A到B。
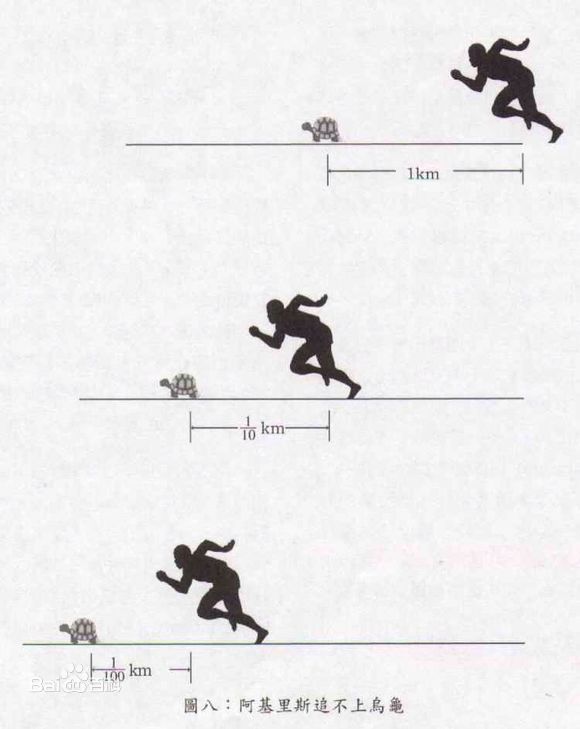
阿基里斯追不上烏龜
“阿基里斯追不上烏龜”是“兩分法”的演化。阿基里斯是古希臘神話中的善於奔跑的英雄。芝諾認為,跑得再快也追不上烏龜,並且永遠追不上烏龜。理由是,追者首先要達到烏龜的出發點,這樣烏龜中是領先一段路。假設烏龜超前1000米,阿基里斯以百倍於烏龜的速度追擊。當阿基里斯跑到烏龜原來的位置時,烏龜前進了10米;當阿基里斯跑完這10米的時候,烏龜又前進了1分米:……照此下去,阿基里斯固然可以不斷的縮短同烏龜的距離,但始終處於烏龜的後面,而追不上烏龜。
飛矢不動
“飛矢不動”。芝諾認為,飛著的箭是靜止的。因為,箭在飛行的某一瞬間,一定處於也只能處於整個飛行軌跡中的一個位置,並且是一個確定的位置上,它不能同時占據兩個位置,具有兩個長度。因此,箭在某一瞬間上是靜止的。箭此時在這個位置上,彼時在那個位置上,整個過程便由一系列的靜止組成,而靜止的總和不能構成運動。
運動場
“運動場”,芝諾認為,一半的時間可以等於一倍的時間。假定有3列物體,其中的一列[A],當其他兩列[C]以相等的速度朝相反的方向運動時是靜止的,在它們都走過了相同一段距離的時間中,超越[C]列物體的數目要比它越過[A]列中物體的數目多一倍。因此它用來越過[C]列的時間要比它用來越過[A]列的時間要長一倍,但是和[C]用來走到[A]位置的時間卻是相等的,所以一倍的時間等於一半的時間。