舒爾乘子(Schur multiplier)是一類特殊的映射,是群的二次同調群。
基本介紹
- 中文名:舒爾乘子
- 外文名:Schur multiplier
設G為有限群,A為任一阿貝爾群,用符號Cz (G; A)表示GXG到A中的所有映射之集,在Cz (G; A)中定義加法如下:對任意的(二,y> EGXG,f,hEC2(G;A),規定(.f+h) (x, y)=f(x,y)+h(x,y),在此加法下CZ (G ; A)成為一個交換群.設BZ(G;A)是由形為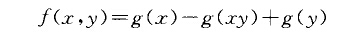
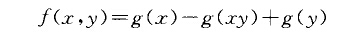
舒爾乘子
的.fECZ(G;A)所生成的子群,其中g為G到A的某一映射.再設Z2 (G; A)是對任意二,y,zEG滿足:

舒爾乘子
的.fEC2(G;A)所生成的子群,從而,BZ
