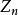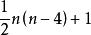閉折線邊之間的交點個數,稱為自交數,但計算自交數時,k條邊相交的點算Ck2個,每條具體的閉折線Zn都有一個確定的自交數θ(Zn),但反之不然:對於一個給定的正整數k,可能有幾個Zn,使θ(Zn)=k,也可能不存在這樣的Zn。由此,θ(Zn)的最小值為0。在1992和1995年楊林和王方漢完成了尋求和證明θ(Zn)最大值的工作。
基本介紹
- 中文名:自交數
- 外文名:self intersection number
- 定義:閉折線邊之間的交點個數
- 所屬學科:數學(幾何學)
- 相關人物:楊林和王方漢
定義,自交數的最大值,
定義
閉折線邊之間的交點稱為自交點。自交點的個數稱為自交數。
計算自交點,兩邊相交的算1個,三邊相交的算3個,……,k邊相交的算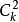 個,n邊閉折線
個,n邊閉折線 自交數記為
自交數記為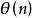 。
。
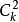

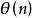
自交數的最大值
如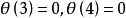 或1,在圖1中,我們畫出了
或1,在圖1中,我們畫出了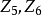 分別具有自交數
分別具有自交數 或5,
或5, 或7的一個圖形。
或7的一個圖形。
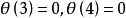
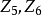


 圖1(a)n=5
圖1(a)n=5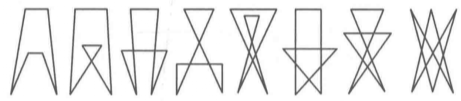 圖1 (b)n=6
圖1 (b)n=6我們知道,n邊閉折線每條邊最多同其他 條邊相交(因同它自身和兩鄰邊不會相交),因此
條邊相交(因同它自身和兩鄰邊不會相交),因此 自交點最多有
自交點最多有 個,就是必有
個,就是必有



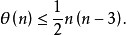
定理1 n邊閉折線的最大自交數
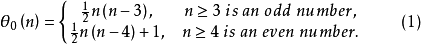
證明:事實上,當 時,只需構造以正n邊形最長的對角線為邊的正n角星即可,如圖2,在
時,只需構造以正n邊形最長的對角線為邊的正n角星即可,如圖2,在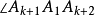 兩側,各有正n邊形的
兩側,各有正n邊形的 個頂點:對
個頂點:對 來說,其右側還多了一個頂點
來說,其右側還多了一個頂點 這樣,就可以連出
這樣,就可以連出 對最長的對角線(每條同
對最長的對角線(每條同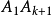 有一個交點):
有一個交點): 。因此,共有
。因此,共有 個交點,考慮所有對角線(總共
個交點,考慮所有對角線(總共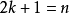 條)
條) 又每個交點算了兩次,因此,交點總數是
又每個交點算了兩次,因此,交點總數是

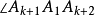




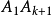


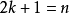


 圖2
圖2 圖3(a)
圖3(a) 圖3(b)
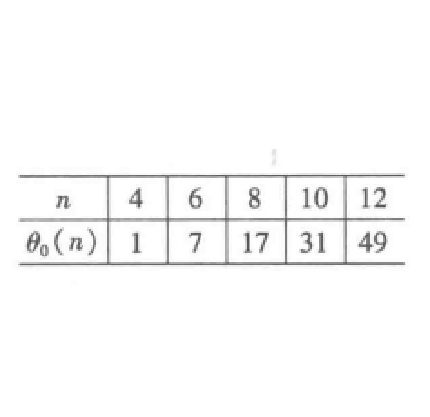
圖3(b)對 ,可用如圖3所示的閉折線(圖中以n=10和12為例),它頂點排列是很有規律的:奇數頂點在上,偶數頂點在下;“星形”是中心對稱的。它有兩條對摺邊
,可用如圖3所示的閉折線(圖中以n=10和12為例),它頂點排列是很有規律的:奇數頂點在上,偶數頂點在下;“星形”是中心對稱的。它有兩條對摺邊 和
和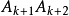 各與
各與 條對角線相交;其餘
條對角線相交;其餘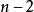 條單折邊各與
條單折邊各與 條對角線相交,而每個交點都被算了兩次,因而交點的總個數為
條對角線相交,而每個交點都被算了兩次,因而交點的總個數為


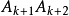

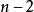


綜合(2)、(3),即得(1)。
如套用調節號 把(1)的兩式合併,即得:
把(1)的兩式合併,即得:

定理2 n邊閉折線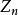 的最大自交數
的最大自交數