聲波的頻率依賴衰減

聲波傳播時，聲壓或介質速度E隨傳播距離x呈現E(x+dx)= E(x)*exp{-α(ω)*dx}形式的衰減。這裡的衰減係數α與聲源角頻率ω的y次冪成正比，即α=α₀ω^y，其中參數α₀>0，且y \in [0,2]。

基本介紹

• 中文名：聲波的頻率依賴衰減
• 外文名：Power-law frequency dependent acoustic wave attenuation(or absorption or dissipation)
• 學科：力學
• 類別：唯象公式、實驗規律

大量實驗和實地測量發現，決定聲波傳播過程中的能量耗散（即衰減）快慢的參數α服從一個由實驗測量數據擬合得到的以頻率為變數的冪函式，即α=α₀ω^y。這裡的ω代表聲源角頻率，介質參數y為0到2的任意實數，介質參數α₀為大於0的實數，y和α₀均可由測量數據擬合得到。很明顯，頻率愈高，耗散愈快。對於理想固體和液體材料，y的值為0或2，即能量耗散不依賴於頻率或與頻率的二次方成正比，例如，水中聲波傳播耗散的y值為2。然而，對於人體組織、聚合物、液晶、土壤、膠體、顆粒物質、多孔岩石、泡沫、紡織物、石油等複雜介質，參數y卻在0到2之間變化。例如，層狀多孔岩石和水下沉積物的y值接近1；各種人體組織的y值在1.1到1.7之間：脂肪為1.7左右，癌組織為1.3左右，結締組織為1.5 。

下圖顯示了雙對數坐標下實驗測量的多孔岩石和牛肝臟中聲波的“頻率—衰減”圖。這裡“shear”和“long” 分別代表剪下波和縱波。圖中直線的斜率即為頻率依賴耗散的冪指數y。例如, 牛肝臟(bovine liver)中的縱波在1–100 MHz範圍內對應的y=1.3；YIG(釔銦石榴石的縮寫) 是一種理想的固體水晶材料, 高頻剪下波和縱波對應的y值都是2；花崗岩1和花崗岩2表示兩種花崗岩，花崗岩1在140 Hz到2.2MHz範圍內縱波對應的y=1。從上述不同介質的聲波衰減實驗數據中，可以看到聲波在複雜介質中傳播時的冪律頻率依賴耗散（衰減）現象。

力學模型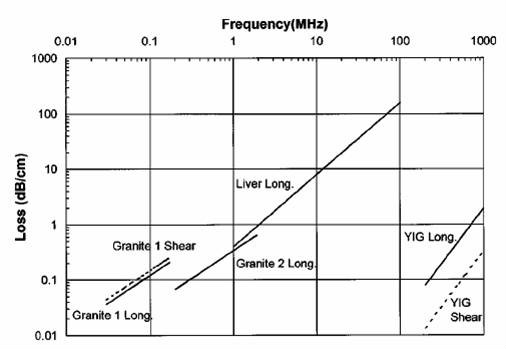

多孔岩石和牛肝臟中聲波的“頻率—衰減”圖

分數階導數聲波耗散模型是描述聲波冪律頻率依賴耗散現象的有力工具之一。