考柯西特圖(Coxeter graph)是一個特殊的圖。它是具有高度對稱性的非哈密頓圖的例子,也是猜想“存在從任長為3的路到另外任一路的自同構”的反例
基本介紹
- 中文名:考柯西特圖
- 外文名:Coxeter graph
- 領域:數學
- 學科:圖論
- 性質:高度對稱的非哈密頓圖
- 提出者:考柯西特
概念,極圖,哈密頓圖,圖論,
概念
考柯西特圖(Coxeter graph)是一個特殊的圖。它是具有高度對稱性的非哈密頓圖的例子,也是猜想“存在從任長為3的路到另外任一路的自同構”的反例(見圖)。考柯西特圖是由加拿大英裔幾何學家霍華德·斯科特·麥克當納·考柯西特提出的,他是20世紀最偉大的幾何學家之一。
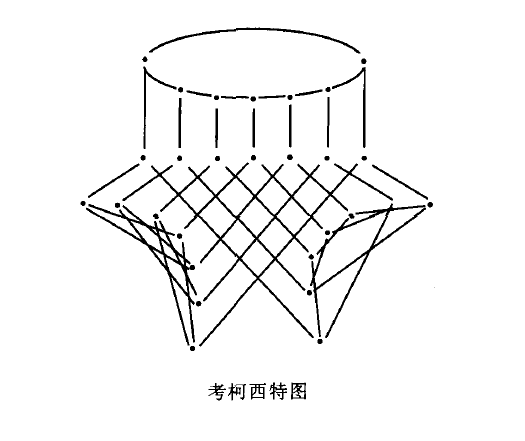
極圖
極圖是一類特殊的圖。指階數一定在某種意義下最大的圖。給定一個圖族L,在所有n階圖中含邊最多,不以L中圖為其子圖的圖。這個給定的圖族L稱為禁用圖類。關於L的全部n階極圖的集記為Ex(n,L),其中每個極圖邊數相等,記為ex(n,L)。例如,Tm,n圖,即有n個節點,各部節點數分別為[n/m](即n/m的整數部分)或[n/m]+1的完全m部圖,就是一個極圖。其中,L是m+1階完全圖.Tm,n常稱為圖蘭圖。事實上,有圖蘭定理:在所有不含完全圖Kn作為子圖的m階圖中,邊數最多的圖只有一個,就是Tm,n-1.它第一次出現在圖蘭(Turn,P.)1941年發表的文章中,由此而得名。
哈密頓圖
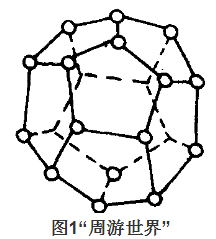
1859年,英國數學家哈密頓提出一種名為“週遊世界”的遊戲。他用正十二面體(如圖1)的20個頂點代表20個大城市,要求沿著棱從一個城市出發,經過每個城市恰好一次,然後回到出發點。
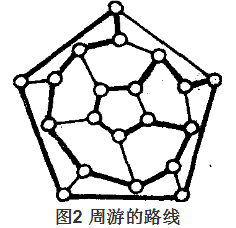
這個遊戲曾經風靡一時。為了清楚起見,我們作一個平面圖(如圖2),與這個十二面體的頂點和棱所組成的圖同構,則圖中粗的邊組成的圈就是一個所求的路線。我們還可以找到其他的路線。
一般地,在一個給定的圖中,若存在一條迴路,經過每個頂點恰好一次,則這個迴路稱為哈密頓迴路;若一個圖中可以找到一個哈密頓迴路,則這個圖稱為哈密頓圖。表面上看哈密頓圖的概念與歐拉圖的概念非常相似,但兩者迥然不同。可以找到一個歐拉圖但不是哈密頓圖的例子,也可以找到一個哈密頓圖但不是歐拉圖的例子。
對哈密頓圖的判定問題,迄今還沒有像歐拉圖那樣能找到一個很漂亮的充分必要條件。奧爾給出了一個很重要的充分條件:G為簡單圖,頂點數n≥3,且對每一對不相鄰的點u,v,有:

圖論
近年來比較活躍的數學分支之一。圖論是研究各種圖的性質和特徵的一門理論,主要包括圖與子圖、圖的連通性、可平面性、正則圖、樹、著色問題、圖的矩陣以及網路等內容。圖論的發展已有200多年的歷史。早在18世紀中葉就已出現有關圖的文字記載。這時的圖論尚處於萌芽階段,多數問題是圍繞著遊戲而產生的,最有代表性的是著名的哥尼斯堡七橋問題(相當於我國的一筆畫問題)。19世紀中葉到20世紀中葉,圖論問題大量出現,諸如哈密爾頓“繞行世界”問題,關於地圖著色的四色問題以及與之有關聯的圖的可平面性等等。在這個階段,也出現了以圖為工具去解決其他領域中一些問題的成果,例如,凱萊把圖論套用到有機化學中關於同分異構物的計數問題,克希霍夫套用樹研究電網路的分析問題等等。20世紀中葉以後,由於生產管理、軍事、交通運輸、計算機網路等方面提出的實際問題的需要,特別是許多離散性問題的出現,以及由於有了大型超高速計算機,而使大規模問題的求解成為可能,圖論及其套用的研究得到了飛速發展。這個階段的開創性工作是以福特和福克遜建立的網路流理論為代表的。圖論和線性規劃、動態規劃等最佳化理論和方法的相互滲透,促進了組合最最佳化理論和算法的研究以及圖論對實際問題的套用,與此同時也豐富了圖論的內容,使圖論的發展更加充滿活力。
