繞射輻射振盪器

電子沿光柵表面運動時，會產生電磁波輻射，這一現象稱為史密斯—帕賽爾效應，根據這一效應研製出了可工作於毫米波、亞毫米波段的新型器件，稱為繞射輻射器件。由於在該類器件中採用了準光學諧振腔和繞射光柵，所以又稱為具有開放式諧振腔和反射光柵的振盪器，簡稱奧羅管（Orotron-Oscillator with Open Cavity and Reflecting Grating）。

基本介紹

• 中文名：繞射輻射振盪器
• 又名：奧羅管
• 類型：一種新型微波管

奧羅管的工作原理

奧羅管的典型結構示意圖如圖1-1所示，其主要組成部分包括由上反射鏡1和下反射鏡2構成的開放式諧振腔，裝嵌在下反射鏡2上的繞射光柵3、電子槍6、收集極5以及能量輸出裝置7等。電子槍產生的薄帶狀電子注4沿光柵表面運動並輻射電磁波。

圖1-1 繞射輻射振盪器結構示意圖

當具有一定速度的電子注沿光柵表面通過時，產生史密斯—帕賽爾效應。如果沒有諧振系統，則這種輻射是不相干的，正是由於奧羅管內有了準光學諧振腔，由史密斯—帕賽爾效應產生的電磁波受到高品質因數的準光腔的頻率挑選作用，才建立起了穩定的相干振盪，從而發展成為一種新型真空電子器件——奧羅管。分析表明，當電子注的速度與光柵上電磁波的相速同步時，可以得到穩定的振盪，這時，電子注將在電場作用下產生群聚，從而可以與高頻場進行有效的能量交換。

若形成光柵的槽的對稱中心線垂直光柵表面，電子注在光柵表面上方平行於表面運動，電子注由光柵產生的電磁輻射經準光諧振腔反饋給電子注，電子注在縱向高頻場作用下就產生群聚。這種電子注與高頻場之間的相互作用不斷進行，最終在系統中建立起穩定的振盪，振盪能量由能量輸出裝置輸出，振盪波長由式（1.1）確定，即

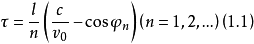
式中，l為光柵的空間周期；c為光速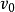；為電子注的縱向速度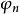；為能量輸出方向角，它是以光柵表面的中點為原點計量的角度。在圖1-1所示的情形下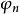，=90°，即能量耦合裝置在上反射鏡的中央，因此，這時由式（1.1）可得振盪頻率和同步電壓為

式中，n為奧羅管的工作模式；為輻射波長。可見，改變，就會改變工作模式n。

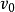
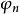
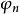
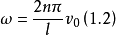
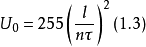
只要改變兩個反射鏡之間的距離，諧振腔的諧振頻率就會隨之改變，因此奧羅管可以利用這一方法實現頻率的機械調諧。在機械調諧過程中，振盪模式也會隨著改變。

奧羅管也會有較小的電子調諧範圍。

奧羅管的特點

奧羅管由於使用的是由互相分離的上、下反射鏡構成的準光學開放式諧振腔作為高頻系統，因此帶來了下述特點。

1、 諧振腔的尺寸不再受與波長共度的限制，使腔的尺寸可以做得很大，這是因為開放腔開敞的側面使一部分模式的能量可以向空間輻射而不再在腔中振盪，使得模式密度大大減少，降低了模式競爭的可能，從而可以利用高次模式作為工作模式而不致因模式競爭而引起工作不穩定。諧振腔尺寸的增大，儲能高、品質因素很高，所以奧羅管適宜於工作在毫米波、亞毫米波段，甚至已向THz波段擴展。

2、 高頻系統尺寸大，相應整管尺寸也可以做得較大，因此對加工精度和工藝的要求可以相對放寬。

3、 電子注尺寸得以增大，特別是帶狀注的橫向尺寸的增大有利於電子注總電流的提高，這使得利用常規的不收斂電子槍的發射水平就可以滿足器件在短毫米波段的起振和正常工作的要求，降低了對電子槍設計，尤其是陰極發射的要求，亦有利於奧羅管向THz波段發展。

奧羅管的準光學諧振腔

在奧羅管中所使用的開放式準光諧振腔，與普通準光學諧振腔的不同之處在於，在下反射鏡中嵌入了一條光柵，正是這一光柵成為了奧羅管中電子注與高頻場換能的機構。圖1-2給出了這種帶有光柵的準光腔的剖面圖，為了簡化，假設準光腔是一個平行平面腔。

圖1-2 具有繞射光柵的平行平面鏡準光腔

在圖1-2中，光柵周期為l，且l<<；光柵由最簡單的矩形槽形成，槽寬為d,槽深為b；兩反射鏡間距為H，且H>>。通常認為結構在x、y方向上是無限擴展的，在這一假定下，腔中的場可近似為一種準平面波。當然，在光柵表面，由於光柵是一種周期性結構，會使得高頻場也成為周期場，並包含有無窮多次空間諧波，也就是說，在光柵表面的場並不能近似成準平面波。但這種空間諧波的振幅將隨離光柵表面的距離增加而迅速衰減，因此在遠離光柵表面的空間，腔內場仍然是一種準平面波。

另外，由於光柵上的場是表面波場，加之光柵表面積的增加，所以光柵的引入必然會增加準光腔的高頻損耗，從而降低了準光腔的品質因素，這是奧羅管用準光腔的一個特點。為了不致引起Q值的過分降低，對光柵的加工精度和光潔度提出很高的要求。

諧振條件和相速

具有繞射光柵的由平行平面反射鏡組成的準光腔的諧振條件可寫為

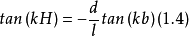
式中，k=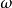/c，為自由空間波數。式（1.4）給出了諧振時繞射光柵尺寸與反射鏡間距之間的關係。

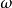
當準光腔不存在光柵時，d=0，b=0，式（1.4）就成為

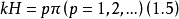
這實際上已成為一般波導諧振腔的普遍諧振條件。

從式（1.1）出發，不難得到存在光柵時，腔中電磁波沿光柵傳播的相速是

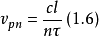
固有品質因數

如果忽略光柵中的儲能，考慮上、下鏡面及光柵的高頻損耗後可得奧羅管準光腔的固有品質因數為

式中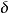，為材料的集膚深度。

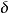
分析表明，當選擇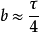,d/l=1/2時，光柵的損耗最小，這時式（1.7）可重寫成

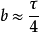
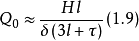
如果沒有光柵，則d=0,b=0,l=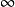，則

模式分隔度

對於共軸球面準光腔，其鏡面附近的波場等相位面與鏡面重合，只有離開鏡面後，波場才會逐漸變為接近於平面波，成為準平面波。其模式以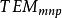表示，m、n是模式的橫向特徵值，分別表示在x、y方向上的場的零值線（節線）個數；而p則是模式的縱向（z向）特徵值，表示場在腔體縱向上的駐波半波長數。

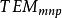
共軸球面腔的諧振頻率為

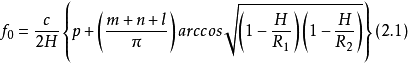
式中，H為兩反射鏡軸線上的間距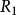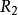；、分別為它們的曲率半徑；c為光速。

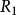
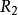
對於共焦腔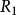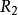，==H,則

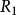
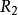
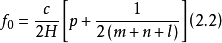
定義兩相鄰模式之間的頻率差為模式分隔度，即模式標號m、n或p中任意一個增加1或減少1時引起的諧振頻率的改變數。由式（2.1）就可以求出模式分隔度的大小，即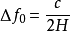(m、n不變，p改變1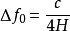）(p不變，m或n改變1)

可見，它們都與頻率無關，而只與腔體尺寸H有關。這是共軸球面準光腔（平行平面腔只是這種腔的一個特例）與普通波導腔的根本區別，也是準光學開放腔更適合毫米波、亞毫米波波段套用的又一個原因。