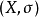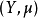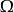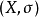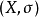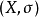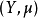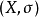基本介紹
- 中文名:緊開拓撲
- 外文名:compact-open topology
- 本質:拓撲結構
- 意義:映射空間上一類常見的拓撲
- 特徵:正則空間
- 相關詞:聯合連續拓撲
簡介,定義,性質,緊開拓撲和聯合連續拓撲的關係,
簡介
緊開拓撲(compact-open topology)一種拓撲結構。是映射空間上一類常見的拓撲。設F為拓撲空間X到拓撲空間Y的映射族,若:

定義
設X、Y為兩個拓撲空間,記C(X,Y)代表X和Y之間所有連續映射的集合。給定X的緊湊子集K和Y的開放子集U,令V(K,U)表示所有函式f∈C(X,Y)的集合,使得f(K)⊂U。然後收集所有 這樣的V(K,U)是C(X,Y)上緊湊開放拓撲的基礎。 (此集合併不總是形成C(X,Y)上拓撲的基礎。)
當在緊湊生成空間的類別中工作時,通常將該定義修改為由作為緊湊豪斯多夫空間的映射K形成的底層來進行修改。 當然,如果X緊湊地產生和豪斯多夫,這個定義與前一個一致。 然而,如果要將緊湊產生的弱豪斯多夫空間的方便類別笛卡爾閉合,其他有用的屬性,修改後的定義是至關重要的。這個定義與上述之間的混淆是由單詞compact的不同用法引起的。
性質
如果*是一個點空間,則可以使用X來識別C(*,X),並且在該標識下,緊開拓撲與X上的拓撲一致。
如果Y是T0,T1,Hausdorff,Regular或Tychonoff,則緊開拓撲具有相應的分離公理。
如果X是Hausdorff,S是Y的子基,則集合{V(K,U):U∈S}是C(X,Y)上的緊開拓撲的子基礎。
如果Y是度量空間(或更一般地,均勻空間),則緊開拓撲等於緊湊收斂的拓撲。換句話說,如果Y是度量空間,則若且唯若對於X的每個緊湊子集K {fn}均勻地收斂於f時,序列{fn}收斂於緊開拓撲中的f。特別地,如果X是緊湊的並且Y是一個均勻的空間,那么緊開拓撲結構等於均勻收斂的拓撲。
如果X,Y和Z是拓撲空間,Y本地緊湊型Hausdorff(或者甚至局部緊湊的規則),則給出組合圖C(Y,Z)×C(X,Y)→C(X,Z)通過(f,g)↦f o g,是連續的(這裡所有的功能空間都是緊湊型開放拓撲,C(Y,Z)×C(X,Y)被賦予乘機拓撲)。
如果Y是局部緊湊的Hausdorff(或不規則)空間,則由e(f,x)= f(x)定義的評估圖e:C(Y,Z)×Y→Z是連續的。這可以看作是上述的特殊情況,其中X是一點空間。
如果X是緊湊的,並且Y是具有度量d的度量空間,則C(X,Y)上的緊湊開放拓撲是可辨別的,並且其的度量由e(f,g)= sup {d f(x),g(x)):x中的x},對於f,g∈C(X,Y)。
緊開拓撲和聯合連續拓撲的關係
定義1 a)設F是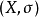 到
到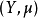 的函式族,令
的函式族,令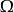 :
: ,對
,對 ,使連續的F的不分明拓撲l稱為聯合連續的;b)F的不分明拓撲la,稱為在的子空間才上聯合連續,如果映射
,使連續的F的不分明拓撲l稱為聯合連續的;b)F的不分明拓撲la,稱為在的子空間才上聯合連續,如果映射 是連續的。
是連續的。