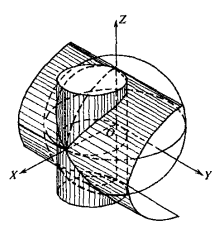
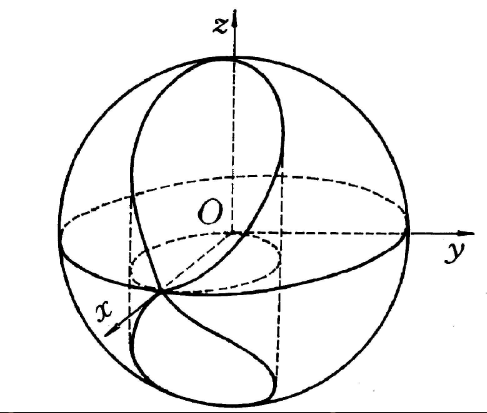
維維亞尼曲線(Viviani curve)是一種特殊曲線，球面x+y+z=a與圓柱面x+y-ax=0的交線。它的參數方程可寫作r(t)=(a cosθ，a cos θ sin θ，a sinθ)，θ∈[0，2π]，是由球面上經度與緯度相等或成相反數的點組成的。維維亞尼(V.Viviani)在整理和修復佛羅倫斯圖書館所藏的東方學者對阿波羅尼奧斯(Apollonius，(P))所著《圓錐曲線論》第5卷的評註時，於1692年正式提出了佛羅倫斯之迷：求一個教堂的半球形屋頂的面積，在屋頂的四面挖去相同的圓孔形窗戶，此即球面與兩個柱面的交線，這個問題曾經引起過許多數學家如約翰第一·伯努利(Bernoulli，Johann Ⅰ)、沃利斯(J.Wallis)和洛必達(L′Hospital，G.-F.-A.de)的重視，特別是早在1689年，萊布尼茨(G.W.Leibniz)還從德國到義大利去會見維維亞尼，並用積分法給出此問題的解法。
基本介紹
- 中文名：維維亞尼曲線
- 外文名：Viviani curve
- 所屬學科：數學
- 所屬問題：立體幾何
- 簡介：球面與圓柱面的交線
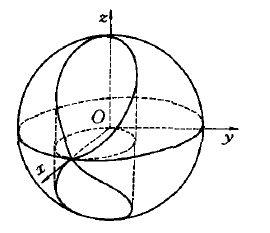
基本介紹,維維亞尼曲線的參數方程,例題解析,
基本介紹
維維亞尼曲線是由方程組
圖1 維維亞尼曲線
維維亞尼曲線的參數方程
由維維亞尼曲線：
圓柱面的方程即方程（2）可以寫為
例題解析
【例1】一個半徑為a的球面與一個直徑為小於球面半徑的圓柱面，如果圓柱面通過球心，那么這時球面與圓柱面的交線叫做維維安尼(Viviani)曲線，這條曲線的方程可以寫為
試求此曲線對三個坐標面的射影柱面方程。 ．
分析 求曲線對於坐標面的射影柱的方程一般通過消變數的方法，這裡要注意變數的範圍。
解 顯見，曲線對xOy面的射影柱面為圓柱面
，
消去y得
從而曲線對xOz面的射影柱面是拋物柱面
滿足
的部分。
消去x得
【例2】求維維安尼(Viviani)曲線
解 所給方程
中不含z，故它就是曲線關於XOY面的投影柱面方程，將其化為
可看出該投影柱面是一個圓柱面，將所給兩個方程相減可得
，可見曲線關於XOZ面的投影柱面是一個拋物柱面，從後一個投影柱面方程解出x，代入前一個投影柱面方程可得
，這就是曲線關於YOZ面的投影柱面(圖2)。
圖2
