維特比算法是一種動態規劃算法用於尋找最有可能產生觀測事件序列的-維特比路徑-隱含狀態序列,特別是在馬爾可夫信息源上下文和隱馬爾可夫模型中。術語“維特比路徑”和“維特比算法”也被用於尋找觀察結果最有可能解釋相關的動態規划算法。例如在統計句法分析中動態規划算法可以被用於發現最可能的上下文無關的派生(解析)的字元串,有時被稱為“維特比分析”。
基本介紹
來源
算法
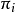


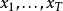
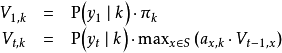
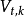
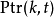
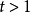
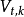
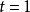
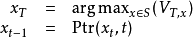
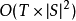
算法基礎
 數學之美維特比算法
數學之美維特比算法C++代碼實現
#include <iostream>#include <string>#include <list>using namespace std;int main(){ double pi[3] = { 0.2, 0.4, 0.4 }; double C[3][3] = { 0.5, 0.2, 0.3, 0.3, 0.5, 0.2, 0.2, 0.3, 0.5 }; double E[3][2] = { 0.5, 0.5, 0.4, 0.6, 0.7, 0.3 }; string output[4] = { "R", "W", "R","W" }; int state[3] = { 1, 2, 3 }; int row = 3; int column = 3; //開闢數組空間 double **delta = new double *[row]; int **path = new int *[row]; int i, j,k; for (i = 0; i < 3; i++) { delta[i] = new double[3]; path[i] = new int[3]; } //將輸出狀態轉為數組 int outnum[4]; for (i = 0; i < row; i++) { if (output[i] == "R") outnum[i] = 0; else if (output[i] == "W") outnum[i] = 1; } //初始化 for (i = 0; i < column; i++) { path[i][0] = 0; delta[i][0] = pi[i] * E[i][0]; cout << delta[i][0] << endl; } //遞歸 for (j = 1; j < row; j++)//序列遍歷,矩陣列遍歷 { for (k = 0; k < column; k++)//狀態遍歷 { double pro = 0; int sta = 0; for (i = 0; i < column; i++)//矩陣行遍歷 { double temp = delta[i][j - 1] *C[i][k]* E[k][outnum[j]] ;//delta[i][j-1]*轉移機率*發射機率 cout << delta[i][j - 1] << " " << E[k][outnum[j]] << endl; cout << temp << endl; if (temp > pro) { pro = temp; sta = i;//記錄路徑信息 } } delta[k][j] = pro; path[k][j]= sta; } } //終止,找到機率最大值 double max = 0; int sta = 0; for (i = 0; i < column; i++) { if (delta[i][row - 1] > max) { max = delta[i][row - 1]; sta = i; } } //回溯,找到最大路徑及其對應的狀態值 list<int> listPath; listPath.push_back(sta+1); for (j = row - 1; j > 0; j--) { sta = path[sta][j]; listPath.push_back(sta+1); } //輸出 cout << "max probability: " << max << endl; list<int> ::iterator itepath; for (itepath = listPath.begin(); itepath != listPath.end(); itepath++) cout << *itepath << " ";}
