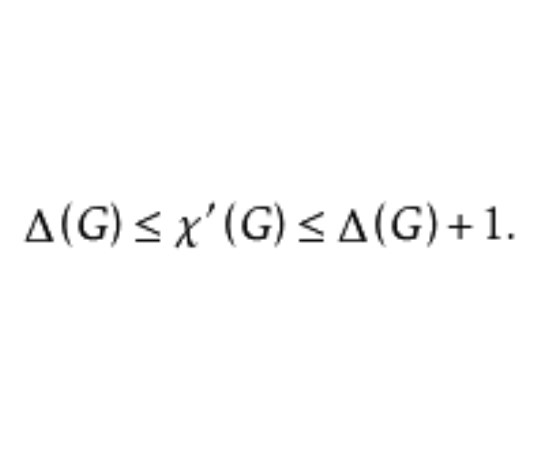維津定理

維津定理(Vizing theorem)是關於圖的邊著色的一個定理，若G是簡單圖，則Δ≤χ′(G)≤Δ+1，其中，Δ表示G上次最大的節點的次，χ′(G)表示邊色數。這個定理是維津(V.G.Vizing)於1964年發表的，由此可以將簡單圖分為二類：對任意簡單圖G，若χ′(G)=Δ，則稱G為第1類圖；否則，稱G為第2類圖。

基本介紹

• 中文名：維津定理
• 外文名：Vizing theorem
• 所屬學科：數學
• 所屬問題：組合學(圖與超圖)
• 簡介：關於圖的邊著色的一個定理
• 提出者：維津(V.G.Vizing)

基本介紹

定理(維津1964) 任何一個圖G的邊色數滿足：

維津定理的證明

證明對圖G的邊數進行歸納證明。如果，結論自然成立，現在假定，而且結論對於邊數較少的圖均成立，現在考慮邊數為的圖G，以下我們對於-邊染色簡稱為染色，而凡是具有顏色α的邊稱為α-邊。

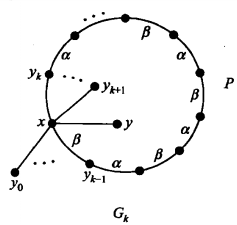圖1

對於任何一條邊，根據歸納假設，G-e有一個染色．在這樣一個染色中，每一個節點v處至多使用了Δ種顏色，因而有一種顏色在v處不出現，對於任何其他一種顏色α，存在唯一一個起點是v的極大的交錯路(注意：這個路可能退化成一個節點)，我們稱其為發自v的交錯路。

假設G沒有染色，那么有下列結論成立：

對於任意邊和任意的的染色，使得α在x處不出現且β在y處不出現，則α一定在y處出現，同時β一定在x處出現，而且這發自y的唯一一條交錯路一定在x處結束。

否則，我們沿著這條交錯路互換α與β的顏色後，可以得到G的一個正常Δ-邊染色，與假定相違。

如圖1，設是一條邊，由歸納假定，具有一個染色(正常Δ-邊染色)c₀。設α為一種在x處不出現的顏色。進一步，設是一個與x相關聯的極大節點序列，使得是c₀中在處不出現的顏色，．對於每個圖，我們可以定義一個染色c_i如下：

如果，且，則；否則，。

注意：在每一個這樣的染色c_i中，x處不出現的顏色與c₀的相同。

現在，設β為c₀中在y_k處不出現的顏色。顯然，β在c_k中也在y_k處不出現，如果β也在x處不出現，我們可以用β給邊染色，從而將c_k擴張成為G的一個染色，因此，在每一個染色中，x處都有一個β色邊與之關聯。由k的極大性，存在一個數，使得。

設P為(c_k中)G_k的一條發自y_k的-路，由於α不在x處出現，由前面的結論，P必定在x處結束，且與x關聯的邊色是α，由於，這一條α就是邊。然而，在c₀和中，(由β的定義和的定義知)β不在處出現，我們考慮(中)的發自的-路P'，由於P'是唯一被決定的，它發自，注意到P上從x到y_k之間的邊上與c_k的染色相同，但是在c₀中，因此也在中，(由β的定義知)不存在β-邊，因此，P'又要在y_k處結束，與前面的結論相違。

維津定理的意義

維津定理的意義在於，根據邊染色規則，所有的有限圖被劃分成為兩部分：如果，則圖是第一類的；否則，是第二類的。怎樣判定一個圖的類型一直是染色理論中的一個基本問題，任何一類非平凡圖類的發現都是很不容易的，目前所知道的基本結論是悲觀的，因為人們已經知道這樣的判定問題是NP-困難的，不過人們仍然在發現一些非平凡的圖類。