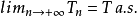絕不可及時(totally inaccessible time)是停時中的一類。停時是一類隨機時刻。指具有某種與將來無關性質的隨機時刻。
基本介紹
- 中文名:絕不可及時
- 外文名:totally inaccessible time
- 領域:數學
- 性質:停時中的一類
- 性質:處處不可預報
概念,停時,可料時,
概念
絕不可及時(totally inaccessible time)是停時中的一類。設T為{Ft}停時,稱T為{Ft}絕不可及時,簡稱絕不可及時,如果對一切{Ft}可料時S,有P({T=S<+∞})=0絕不可及時的直觀意義是:除去一個零概集外,絕不可及時T不能與任何可料時S在有限處相觸及。它在{T<+∞}上是幾乎處處不可預報的。
停時
停時是一類隨機時刻。指具有某種與將來無關性質的隨機時刻。確切地說,對於給定的σ代數流{Ft}t∈R+,如果對任意t∈[0,+∞),有{T≤t}∈Ft,則函式T:Ω→[0,+∞]稱為{Ft}停時。停時有如下的直觀解釋:Ft可理解為某過程在時刻t以前的全部信息,而T則是聯繫於過程的某隨機事件的發生時刻。停時的條件就是“該隨機事件在t以前發生”的事件完全取決於過程在時刻t以前的信息Ft。例如,在離散情形,當一賭徒決定當他勝一百次即停止賭博時,他停止賭博的時刻τ是一隨機變數,事件{τ=n}表示他賭到第n次恰好勝一百次。τ是否等於n當他賭到第n次後即可決定.若Fn包含第n次賭博以前(含第n次)有關賭徒勝負的全部信息,則{τ=n}∈Fn,即τ是一{Fn}停時。
停時又稱可選時或馬爾可夫時或與將來無關的隨機變數。
可料時
可料時是停時中的一類。定義在Ω上的非負函式T稱為{Ft}可料時,簡稱可料時。如果[T,+∞)(即集合{(t,ω):T(ω)≤t<+∞})為Ft可料集。可料時必為停時。一切可料時都是幾乎處處可預報,即若T為可料時,則存在一列上升停時(Tn)n∈Z+,ᗄn有Tn≤T且在{T>0}上有Tn<T a.s。以及: