在每個元件都是剛性的前提下,結構承受任意形式的載荷後能保持原有幾何形狀的特性。
基本介紹
- 中文名:結構的幾何不變性
- 外文名:geometrical invariability of structure
- 領域:力學
分類
機構
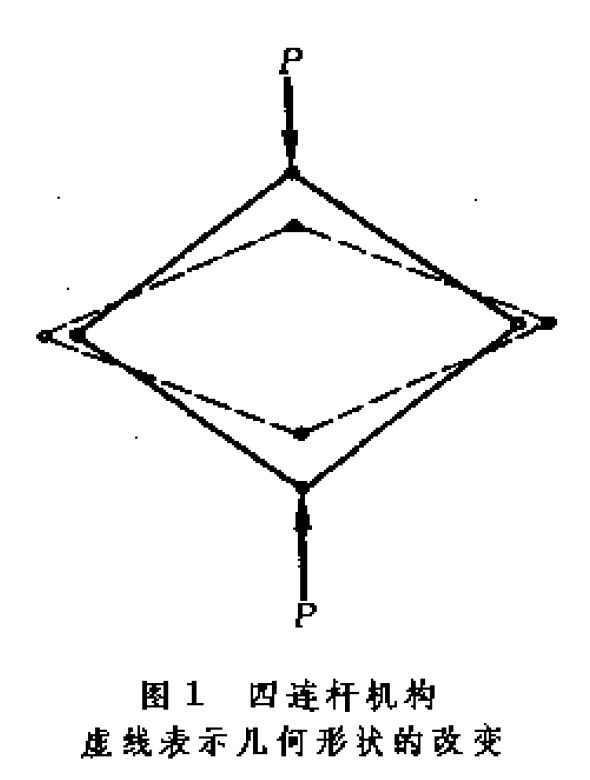
結構

瞬時可變結構

判斷方法
組成法
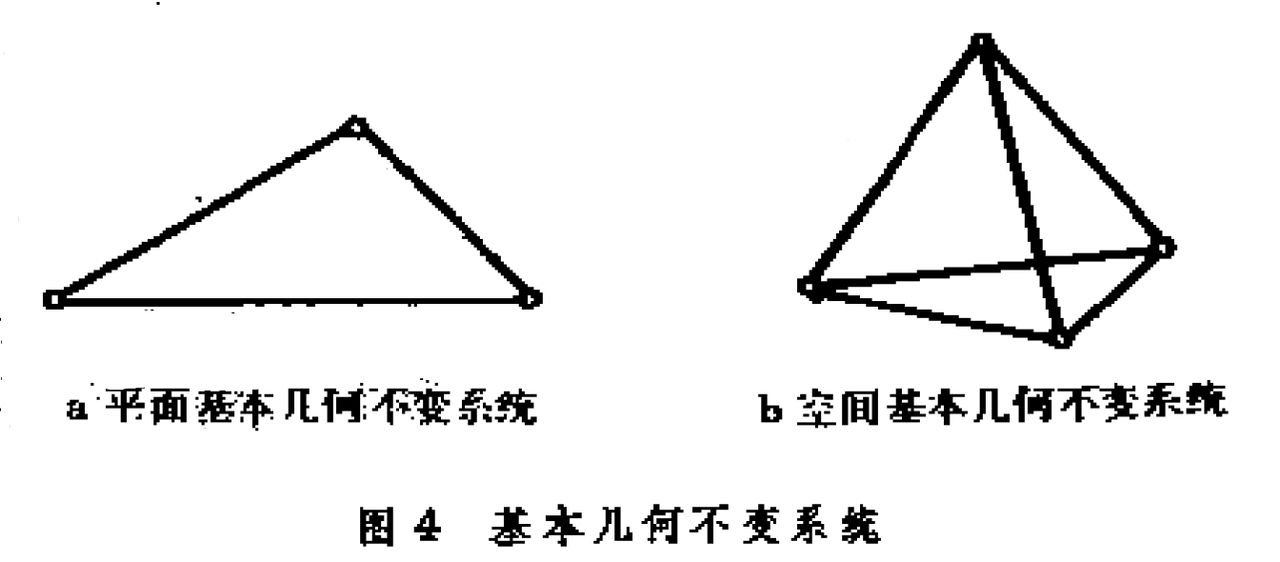
桿和鉸鏈關係法


平衡判斷法
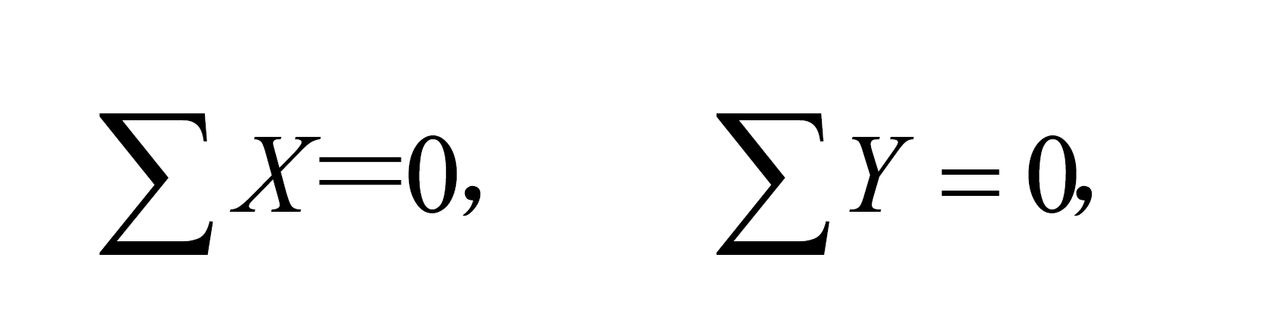
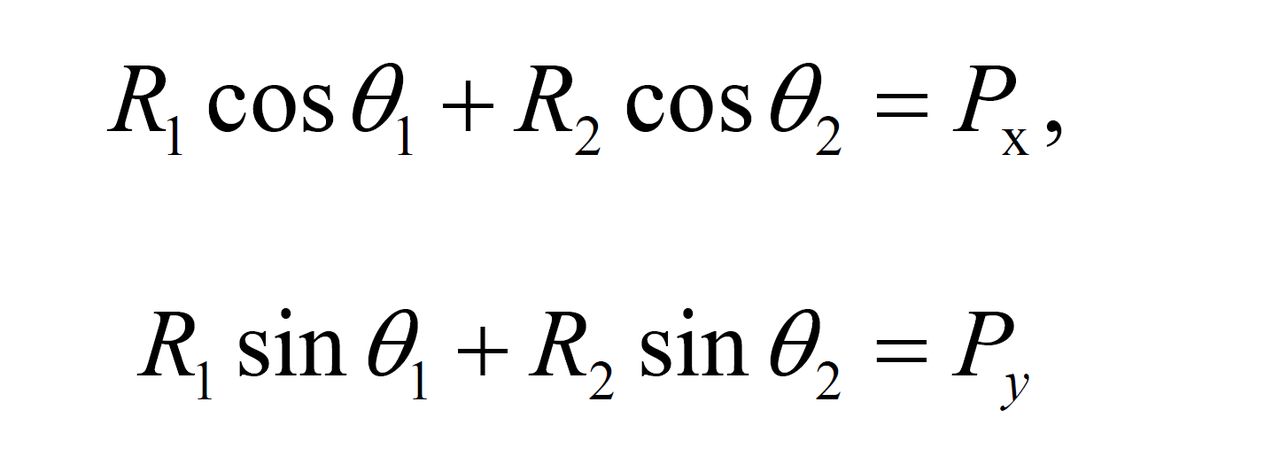
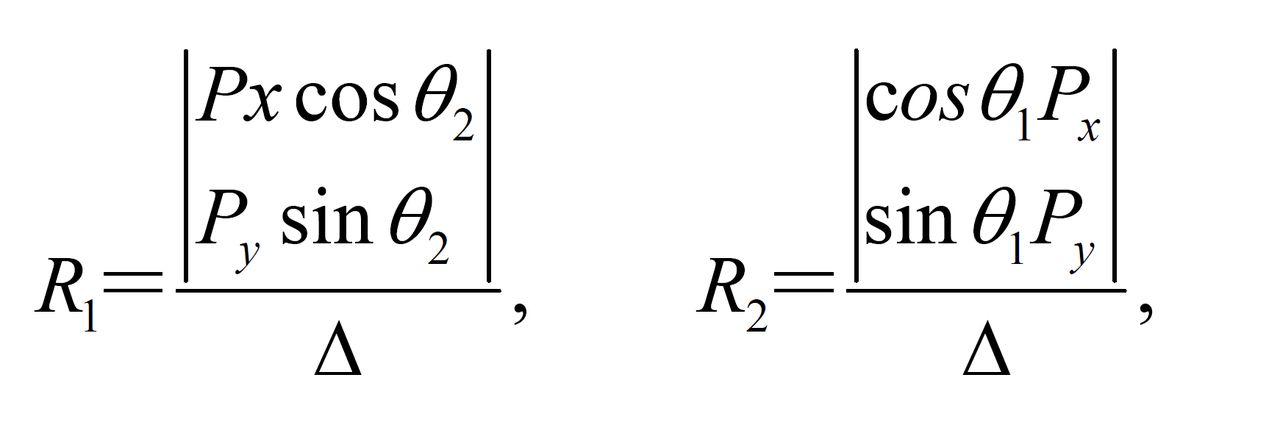

在每個元件都是剛性的前提下,結構承受任意形式的載荷後能保持原有幾何形狀的特性。






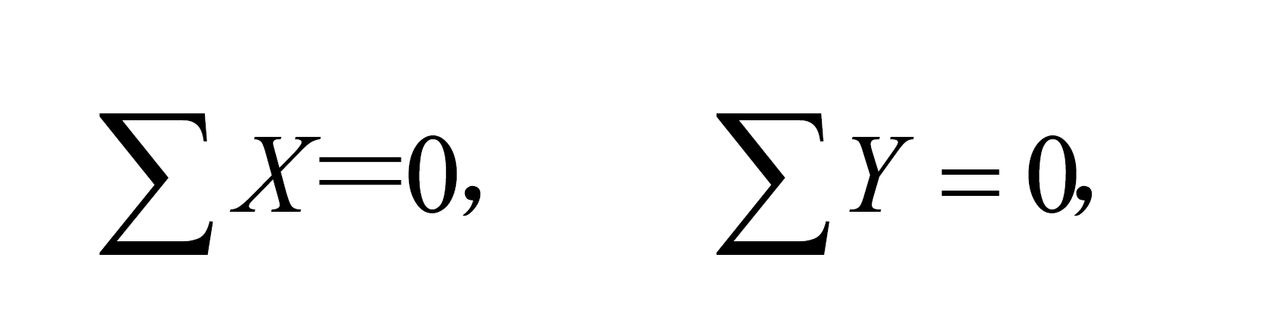
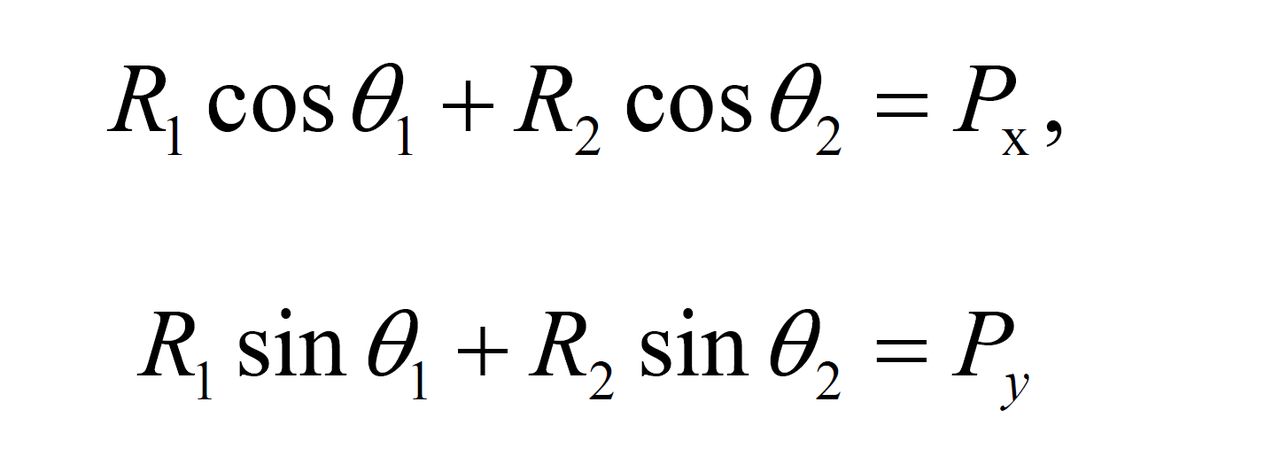
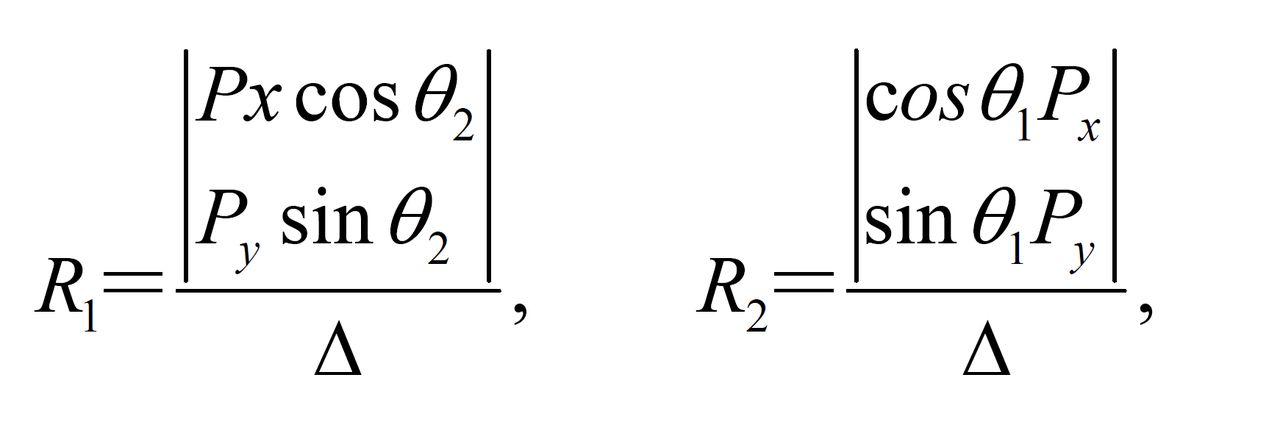

在每個元件都是剛性的前提下,結構承受任意形式的載荷後能保持原有幾何形狀的特性。...... 結構的幾何不變性組成法 不在一直線上的三個鉸接桿所組成的平面系統是最...
幾何不變體系是在建築學裡體系受到荷載作用後,在不考慮體系材料應變的前提下,能保持其幾何形狀和位置不變,而不發生剛體形式的運動體系。幾何不變體系可分為無多餘...
tixi de jihe gouzao fenxi 體系的幾何構造分析 geometric stability of framed structure 由若干桿件相互聯結可組成一桿件體系,若不考慮材料的彈性變形,在任意荷載...
靜定結構是指僅用平衡方程可以確定全部內力和約束力的幾何不變結構。因為靜定結構撤銷約束或不適當地更改約束配置可以使其變成可變體系,而增加約束又可以使其成為有...
第一章 平面結構的組成分析 第一節 結構的幾何不變性 第二節 平面結構組成的基本規則 第三節 平面幾何不變體系的判別示例 第四節 靜定結構和超靜定結構 習題...
全書首先介紹了飛行器結構的發展過程以及設計思想的演變。隨後介紹了桿件(特別是...第3章 靜定薄壁結構的內力分析3.1 幾何不變性和不可移動性3.2 桁架結構...
橋樑結構從有無多餘約束可分為靜定橋樑結構和超靜定橋樑結構。靜定橋樑結構是無多餘約束的幾何不變體系,支座反力及內力可由靜力平衡條件確定。最常見的靜定橋樑...
結構塑性極限是塑性力學的研究內容之一,研究結構在塑性極限狀態下的特性,亦稱結構破損分析。當作用在結構上的載荷增大至某一極限值時,理想塑性材料結構將變成幾何可變...
結構塑性極限分析,又稱結構破損分析,是對結構在塑性極限狀態下的特性的研究,塑性力學的研究內容之一。當外載荷達到某一極限值時,結構即變成幾何可變機構,變形無限制...
3.27 常用結構體系(122)3.27.1 桁架(122)3.27.2 剛架(122)3.27.3 連續梁(124)3.28 靜定和幾何不變性(124)3.29 靜定結構的反力計算(125)...
在進行結構分析之前,須對實際結構進行合理的簡化,確定計算模型,還要進行幾何構造分析,以保證桿系結構的幾何不變性(見結構的幾何不變性)。對於由若干平面桿繫結構...
本書首先介紹微分幾何的基礎知識和非歐幾何的基本定理。然後系統論述狹義相對論與非歐幾何的關係,將物理上的間隔不變性與幾何上的線元不變性聯繫起來,並以此為基礎...
零載法是結構力學中對體系幾何組成分析的一種方法。用來判定體系是否為幾何不變體系。在一些較複雜的結構體系中,去處二元體和兩剛片法等不易判定,可用零載法來判定...
格線殼屋面簡稱網殼結構,網殼結構即為網狀的殼體結構,是格構化的殼體,或者說是...根據邊長小,正多邊形面積小、幾何不變性好(最好是三角形)等要求,選用球內最大...
靜定反力,指靜定結構的反力。靜定結構的受力分析是結構計算的重要基礎。靜定結構是一種類型的結構體系,指無多餘約束的幾何不變體系。其內力及支反力可由平衡...
2.1網架結構的形式 2.1.1網架結構的幾何不變性分析 2.1.2網架結構的形式和選用 2.1.2.1雙層網架的形式和選用 2.1.2.2三層網架的形式 2.1.3格線尺寸和...
由於開截面薄壁梁的厚度t較小,故I很小,因而抗扭能力極低。在自由扭轉的情況下,可認為它是不能承受扭矩的幾何可變系統(見結構的幾何不變性)。②單閉截面薄壁梁...
架的運動圖形成四連桿機構或四連桿鉸鏈機構,用來保證受力系統的幾何不變性和收...g.收放結構的零件之間須有足夠的間隙。 [1] 起落架收放機構相關故障 編輯 ...
1.4 機架桿系結構類型19-5 2 機架桿系的幾何不變性19-5 2.1 平面桿系的組成規則19-6 2.2 平面桿系的自由度計算19-6 2.2.1 平面桿系的約束類型...
