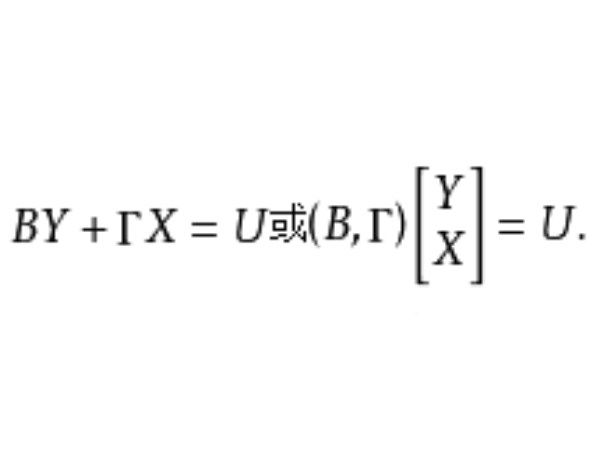結構式識別是從模型的結構式出發，運用“秩條件”討論經濟計量模型識別問題的一種方法。識別系指由簡式推算模型結構參數可能性的討論。若由簡化式參數可以估算出結構參數，稱為可識別，包括正確識別(唯一確定)和過度識別(不唯一確定)；反之，則稱為不可識別。如果需要討論結構參數的變化特性，一般的討論順序是：樣本數據→簡化式係數→“舊”的結構參數→“新”的結構參數。若由簡化式係數不能估算出結構參數，那么上述研究過程便無法進行。所以，模型的識別問題是一個十分重要的問題，應該在進行任何估計以前優先考慮。“秩條件”是模型可識別的一個等價條件，即包含m個方程的線性模型中任一方程可識別等價於其他m-1個方程的變數係數至少可以找到一個非零的m-1階行列式，而聯立方程模型的每一個方程可識別定義了整個模型的可識別。套用本法的一般步驟為：(1)把模型的結構式改寫成隱式函式的形式，略去隨機項；(2)在係數矩陣中刪去正在研究的識別方程的那行係數；(3)刪去待識別方程中的非零係數的那些列；(4)試分析剩下的係數矩陣中有沒有m-1階非零行列式。如果存在，則方程是可以識別的；(5)在方程是可識別的情況下，還需根據它不包含的變數數目(其他方程包含)大於或者等於m-1來確定是過度識別或正確識別。
基本介紹
- 中文名：結構式識別
- 所屬學科：數理科學
- 所屬問題：數理統計
- 相關概念：秩條件，階條件，結構式模型等
基本介紹,結構方程識別的階條件,結構方程識別的秩條件,套用舉例,
基本介紹
如果結構方程中包含了模型中的所有變數，則該方程與模型中任何一個方程的線性組合都與該方程有相同的統計形式，因而該方程一定是不可識別的。這一事實表明，如果一個結構方程可以識別，則必然有若干個變數被排斥在該方程之外。由此可以給出判別結構方程識別性的階條件。
模型的結構式表示為：
其中含有g個內生變數，k個前定變數，以及g個方程，因此它是完備的模型。假定其中第i個結構方程中所含的內生變數的個數為
，前定變數的個數為是
，矩陣
為從模型係數矩陣
中去掉第i行，並去掉第i個結構方程包含的內生變數所對應的列而形成的矩陣。對結構式模型中第i個結構方程的識別條件是：
結構方程識別的階條件
結構方程識別的階條件（完備的結構型）
記M為結構模型中內生變數和前定變數的總個數（M=g+k），
為第i個結構方程中所含變數（內生變數和前定變數）的個數：
。
當第i個結構方程是可識別時：
若
，或
，稱階條件成立，此時如果第i個結構方程可識別，則第i個結構方程是恰好識別的；
若
，或
，稱階條件成立，此時如果第i個結構方程可識別，則第i個結構方程是過度識別的；
若
，或
，稱階條件不成立，則第i個結構方程一定不可識別。
需要指出的是，識別的階條件只是結構方程可識別的一個必要條件，而非充要條件。即如果階條件不成立，則對應的結構方程不可識別；如果階條件成立，則對應的結構方程是否可識別不能確定，還需進一步通過秩條件判別。
結構方程識別的秩條件
識別的階條件實際上是要求某個特定方程排斥（即不包含）一定數目的變數，以保證達到其在統計形式上與模型中其他方程不同的目的。但是，它不能保證模型中的另一個方程也排斥完全相同的變數，如果這樣將與待定方程具有相同的統計形式。所以，階條件只能作為識別的必要條件。
識別的秩條件則是一個充分必要條件，其具體內容為：
在具有g個方程的結構式模型中，任何一個方程能夠被識別的充分必要條件是：該方程被排斥變數結構參數矩陣的秩為g-1。或者說，該方程被排斥變數的結構參數矩陣中，至少有一個g-1階的非零行列式。
若秩
，則第i個結構方程不可識別。
若秩
，則第i個結構方程是可識別的。
其中秩條件是判斷對應結構方程可否識別的充分必要條件，
，則秩條件成立，則對應的結構方程一定可識別；
，則秩條件不成立，則對應的結構方程一定不可識別。利用秩條件可以判別結構方程是否可識別，但不能確定是恰好識別還是過度識別。
識別的秩條件實際上是要求某個特定方程所排斥的變數，必須以不同的統計形式出現在其他g-1個方程中，這樣才能保證模型中的其他方程或這些方程的線性組合與待定方程具有不同的統計形式。
套用舉例
設某聯立方程結構式模型如下：
其中Y、C、I為內生變數，g=3;
和觀察值始終取1的虛變數，D為預定變數，k=3。其結構式參數矩陣為：
對於第二個結構方程：
第三個方程是平衡方程，不存在識別問題。所以該聯立方程模型是可以識別的。
通過此例可以發現結構式方法要比簡化式方法更簡單，因而也更常用。
