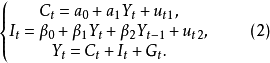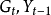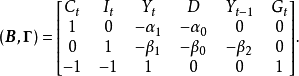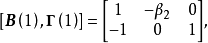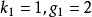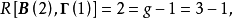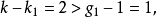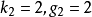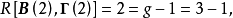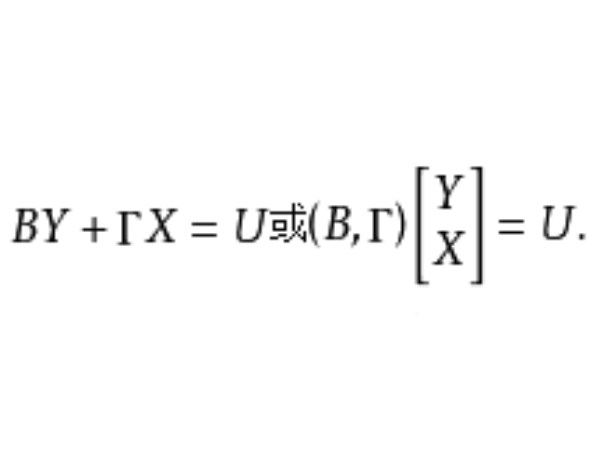結構式識別是從模型的結構式出發,運用“秩條件”討論經濟計量模型識別問題的一種方法。識別系指由簡式推算模型結構參數可能性的討論。若由簡化式參數可以估算出結構參數,稱為可識別,包括正確識別(唯一確定)和過度識別(不唯一確定);反之,則稱為不可識別。如果需要討論結構參數的變化特性,一般的討論順序是:樣本數據→簡化式係數→“舊”的結構參數→“新”的結構參數。若由簡化式係數不能估算出結構參數,那么上述研究過程便無法進行。所以,模型的識別問題是一個十分重要的問題,應該在進行任何估計以前優先考慮。“秩條件”是模型可識別的一個等價條件,即包含m個方程的線性模型中任一方程可識別等價於其他m-1個方程的變數係數至少可以找到一個非零的m-1階行列式,而聯立方程模型的每一個方程可識別定義了整個模型的可識別。套用本法的一般步驟為:(1)把模型的結構式改寫成隱式函式的形式,略去隨機項;(2)在係數矩陣中刪去正在研究的識別方程的那行係數;(3)刪去待識別方程中的非零係數的那些列;(4)試分析剩下的係數矩陣中有沒有m-1階非零行列式。如果存在,則方程是可以識別的;(5)在方程是可識別的情況下,還需根據它不包含的變數數目(其他方程包含)大於或者等於m-1來確定是過度識別或正確識別。
基本介紹
- 中文名:結構式識別
- 所屬學科:數理科學
- 所屬問題:數理統計
- 相關概念:秩條件,階條件,結構式模型等
基本介紹
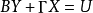
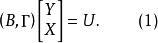
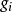
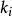

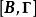
結構方程識別的階條件
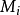


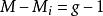
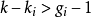
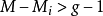

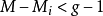
結構方程識別的秩條件
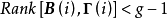
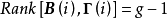
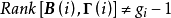
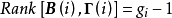
套用舉例