如果系統所有的狀態變數的運動組成整體，各部分的搭配和安排都可以在指定的時間內由容許的輸入來影響和控制而由任意的初態達到原點。
基本介紹
- 中文名：結構可控性
- 外文名：Structural controllability
- 分類：複雜系統
簡介,套用,
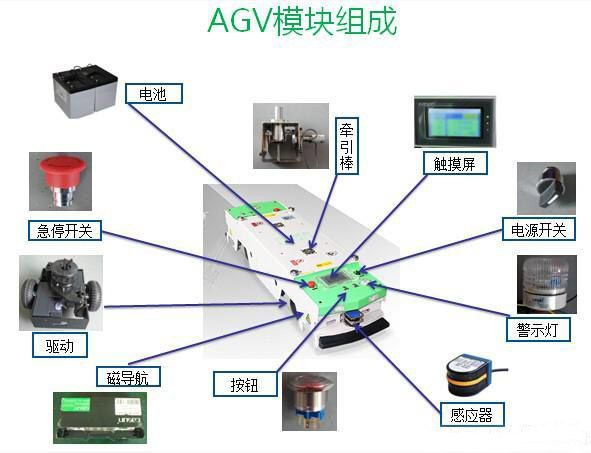
簡介
在對有關靜態網路結構可控性研究進行歸納總結的基礎上，進一步提出時效網路結構的可控性研究方法。首先，通過改進後的最大匹配方法，初步揭示出時效網路的可控性特徵；其次，通過將時效網路映射到LTV系統，給出研究時效網路結構可控的規範框架；最後，在此框架的基礎之上，進一步分析了單節點控制器情形下的網路節點控制中心性的上下界。
靜態網路的結構可控性
若將線性定常系統的系統矩陣S換成由一個表示網路拓撲關係的鄰接矩陣A，其中A′為網路鄰接矩陣A的轉置。從數學形式上比較改寫前後兩種表達形式，它們本 質上並無多大區別，都是一個一階線性常微分方程(組)，但從物理意義上比較，兩者意義相去甚遠：1)前者的矩陣S為系統矩陣，整個表達式描述的是系統自身參數之間的相互影響和變化關係，這樣的x(t)被稱為參數空間；2)後者的矩陣A為鄰接矩陣，整個表達式描述的是網路群體中各個個體之間的相互影響關係，這樣的x(t)被稱為網路空間。
在這裡，後者描述的正是網路結構可控性的問題，可進一步分為兩大類：第一類為判定問題，即給定輸入位置信息(輸入矩陣B)和輸入控制器數目(輸入向量u(t))，判定網路是否結構可控；第二類為最佳化問題，可細分為：1)在網路結構可控的前提下，給定適當的輸入位置信息(輸入矩陣 B)來最小化輸入控制器數目(輸入向量u(t))。2)在網路結構可控的前提下，給定適當的輸入控制器數目(輸入向量u(t))來簡化輸入位置信息(輸入矩陣B)。
結構可控性———從時效網路到特徵子圖
研究時效網路結構可控性不能從原有的思路出發，必須有新的方向和方法。基於此，先提出了最大優先匹配方法(PMM)。
基於定義，將一個時效網路分割成一系列的特徵子圖，然後從中提取出最大特徵子圖，最後利用這些最大特徵子圖來研究時效網路的結構可控性問題，具體描述為3個步驟：1)根據時效網路的特徵時間TC將其劃分為一個個特徵片刻IC(特徵片刻中網路的拓撲是靜態的)，在每個特徵片刻中提取出網路的特徵子圖，然後從這些特徵子圖集合中提取出所需要的最大特徵子圖。2)將所有的節點按照一定的優先權進行排序得到優先序列，給出3種具有代表性及可比性的優先權排序法：節點出現頻率排序，這是根據局部信息來進行的排序；節點影響力排序，這是根據全局信息來進行的排序；完全隨機排序。3)根據最大匹配的方法從優先序列VP由左向右逐個選取節點，以保證最大特徵子圖的結構可控性。
通過這樣一種轉換，將原來需要在時效網路上直接研究的問題轉換到一系列靜態子圖上來研究，使得時效網路結構可控性的研究簡單直觀，且不需要在方法上做出較大的變動，仿真結果也說明 PMM方法很好地保留下原時效網路的時效特徵。
套用
基於精餾過程的可控性問題，介紹了一種適用於非線性系統的結構可控性分析方法，本方法克服了傳統控制中可控性判斷方法的缺點，不用計算具體數值，只需知道系統各元素之間的變化關係即可。形式簡單，便於工程設計階段套用。對精餾過程的結構可控性所作的分析給出了控制方案、控制變數的選擇方法，為分析系統間的變數關係提供了一種新的途徑。
結構可控性判定方法
Lin給出了一種判斷狀態結構可控性的因果關係圖解法，介紹一種結構簡單，直接利用系統狀態空間矩陣形式的可控性圖解分析方法，其步驟如下。
1、寫出系統的狀態空間型結構矩陣，AS矩陣(ASn×n)對角線的右上方每一行都是其他狀態或輸入對本行狀態變數的影響因素，每一列都是某一狀態對別的狀態的 影響。AS矩陣對角線的左下方每一行都是本行狀態的影響因素，每一列的元素或者是本列狀態對別的狀態的影響因素，或者是本列狀態對輸出的影響因素。
2、狀態可控性：對狀態可控性進行分析，可按因果關係由BS各元素到AS對角線(元素)畫關聯線(只能是水平或垂直的連線)， 再由AS對角線到其非 對角相關元素畫關聯線。
3、系統輸出函式可控性分析：對系統輸出函式可控性的分析，在上述關聯線的基礎上，再由AS的各對角線畫到被控輸出的關聯線，若從輸入到輸出有p個互不相重的關聯線，則系統是結構上函式可控的。
4、不可測輸入：對可控性分析時，可不考慮不可測輸入。分析並沒有要求被分析的系統是線性的，因此它也可以用於非線性系統。由非線性系統得到其結構矩陣AS，BS，FS，CS，DS後，就可使用上述分析方法。
精餾塔的可控性分析
按照結構可控性分析規則，發現選用LR和其他任一可測輸入均可以得到狀態完全可控的結論。對於精餾塔頂控制，比較理想的是維持塔頂溫度一定(從而保證塔頂產品質量)，同時保持分離罐液位變化不大，以此兩變數作被控量，選用LR和其他任一可測輸入均可使輸出可控，可能的輸入選擇有：
1)LR，Vf；2)LR，LD；3)LR，p；4)LR，T4 。
一般比較好的選擇是1)， 調節塔頂 回流和分離罐不凝氣流量，這種方案已在實際生產中得到了廣泛的套用。對於方案2)， 塔頂產品產 量一般要求穩定，不適宜作為操作變數。必須要求壓力可調節(而調節壓力可能引起塔壓波動，工藝上不允許)、溫度可調節(工藝設計時一般考慮不到這一點)，因此一般不考慮這兩種控制方案。當然，結構可控性判定方法也有它的局限性。結構可控性判定方法只解決了裝置是否可以被控制的問題，它只給出變數間的關聯關係，而關聯的大小和作用方向並未指明。
例如對於耦合對象，雖然判斷結果可能是可控的，但具有不可操作性。在某些特殊情況下，結構性分析方法並不能適用，例如在傳遞函式間含有零、極點相消情況下，系統是不完全可控的。因此，結構可控性分析方法有一定適用範圍，系統結構可控必須滿足下述兩個條件：1)結構圖上每一個狀態點都可由至少一個控制點達到；2)系統的廣義秩為n。
