基本介紹
- 中文名:索末菲展開
- 外文名:Sommerfeld expansion
- 提出者:阿諾德·索末菲
簡介,索末菲展開的推導,
簡介
在熱力學beta的值較大的情況下,我們可以把以下形式的積分關於 展開為:
展開為:













索末菲展開的推導
我們先作變數代換 :
:






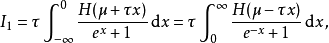
































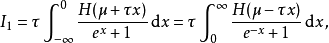













索末菲展開是由阿諾德·索末菲發展的一種近似計算方法,專門用於計算在凝聚態物理和統計物理中出現的一類特定的積分。在物理中,這類積分表示的是採用費米-狄拉克...
阿諾德·索末菲(1868年12月5日~1951年4月26日)生於東普魯士的柯尼斯堡,卒於巴伐亞的慕尼黑。德國物理學家,量子力學與原子物理學的開山鼻祖人物。他對原子結構及...
5.2.1 索末菲展開5.2.2 金屬中自由電子的比熱容5.2.3 金屬的電導率和熱導率5.2.4 電子從金屬表面的熱發射5.2.5 霍爾效應5.3 第十四講課程提綱...
附錄E 索末菲展開 參考文獻 索引 [2] 參考資料 1. d波超導體 .豆瓣[引用日期2016-10-08] 2. d波超導體 .科學出版社[引用日期2014-12-27]詞條...
5.2.1 索末菲展開515.2.2 金屬中自由電子的比熱容515.2.3 金屬的電導率和熱導率525.2.4 電子從金屬表面的熱發射525.2.5 霍爾效應525.3 第十四講...
