概念
米海利斯-曼恬理論 Michaelis-Menten’s theory
米海利斯(L.Michaelis)和曼恬(M.L.Men-ten,1913)提出來的酶反應速度的理論。
基本介紹
- 中文名:米海利斯-曼恬理論
- 外文名:Michaelis-Menten’s theor
- 性質:專業術語
- 套用:社會哲學
修正後理論,適用範圍,
修正後理論
後來由布里格斯(G.E.Briggs)和霍爾丹(J.B.S.Halda-ne)加以修正。它的主要內容是酶E和底物S之間生成中間複合物ES(酶底物複合物enzyme-substra-te complex),假定由於它的分解發生反應而得到產物P,推導出酶反應速度與底物濃度的關係。今對各反應階段如果符合質量作用定律(k+1,k-1,k+2分別是速度常數),在濃度為〔S〕時,則可得到關於將v/V對1n〔S〕作圖,則可得到可v/V=1/2處為折點的s形曲線,在Km值遠為低的底物濃度範圍內反應速度和底物濃度成正比。隨著底物濃度增大反應速度增加的比例變少,終於在〔S〕>>Km時達到恆定的最大速度V。這時酶或酶反應系統就底物來說被飽和了。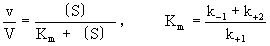
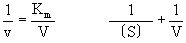
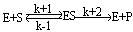
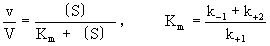
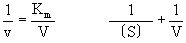
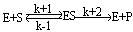
適用範圍
林威沃(H.Lineweaver)和貝爾克(D.Burk)(1934)提出,上式的變式把1/v對1/〔S〕作圖得到直線,用此方法由實驗值求V和Km是方便的(Lineweaver-Burk作圖)。Km稱為米海利斯常數,它的大小和濃度相同,一般用M表示,它的值和酶反應速度成為v=(1/2)V那樣的半速底物濃度(半飽和底物濃度)在數值上是一致的。Km值越小(大),則此酶反應越被低濃度(高濃度)的底物所飽和。這可以說是酶對其底物具有強或弱的結合的親和力。按照來海利斯等原來的說法,假定上式中k-1>>k+2,則Km=k-1/k+1,即Km被解釋為表示ES複合物的解離常數Ka,這在酶化學的許多文獻中有這樣的情形是不少的。米海利斯的模式除了說明原來的對象是酶反應之外,也為一般記述、整理生物現象的一種形式,具有極廣闊的適用範圍。
