米哈依洛夫穩定判據(Michailov stability cri- terion)根據特徵曲線來判斷線性定常系統穩定性的一種準則.它的理論基礎是幅角原理.考慮閉環系統的特徵方程式
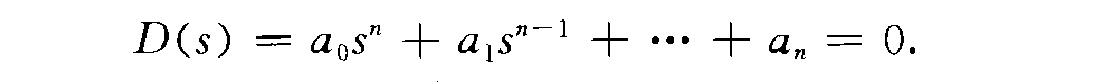
向量D(jcu)端點在複平面上的軌跡稱為D(jcu)的特徵曲線,又稱為米哈依洛夫曲線. 幅角原理說明:當。由一二變到oo時,D<)w)幅角的變化值等於D(s)=0的位於左半開、平面的根的數目((n-m)與位於右半閉、平面的根的數目m 之差乘上n.閉環系統穩定的充分必要條件是:特徵多項式所有的根都在左半開,平面.相應地,幅角變化由下式表示:
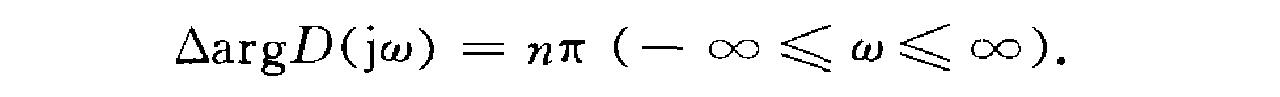
據此,米哈依洛夫穩定判據可表述為:閉環系統的特徵多項式為D(s),若向量D(jm)的幅角變化值在。由一oo變到。時等於nn,其中n是D(s)的次數,則閉環系統是穩定的.通常,此判據也可表述為:當。由。變到oo時,向量D(jm)轉過角度nn/2,則閉環系統為穩定;或當。由。變到二時,特徵曲線由正實軸開始,沿逆時針方向依次通過n個象限,則閉環系統為穩定.當特徵曲線穿越坐標原點,同時轉過((n-1) 個象限,那么系統處於穩定邊緣.
