節點中心性

衡量網路中節點的重要性。網路中一個節點的價值首先取決於這個節點在網路中所處的位置，位置越中心的節點其價值也越大。

基本介紹

• 中文名：節點中心性
• 外文名：Centrality
• 適用領域：網路分析
• 所屬學科：網路科學
• 別名：節點重要性

無向網路節點中心性排序指標

度中心性

度中心性（Degree Centrality）是刻畫節點中心性的最直接的度量指標，即一個節點的度越大就意味著這個節點越重要。無向網路中節點的度定義為與節點直接相連的邊的數目。一個包含個節點的網路中，節點最大可能的度值為，對度為的節點歸一化後，度中心性值定義為：

介數中心性

介數中心性（Betweeness Centrality）是以經過某個節點的最短路徑的數目來刻畫節點重要性的指標。介數刻畫了節點對於網路中節點對之間沿著最短路徑傳輸信息的控制能力。

其中，為從節點到節點的最短路徑的數目，為從節點到節點的條最短路徑中經過節點的最短路徑的數目。對於一個包含個節點的連通網路，節點度的最大可能值為，節點介數的最大可能值是星形網路中的中心節點的介數值：

基於上式，歸一化介數定義為：

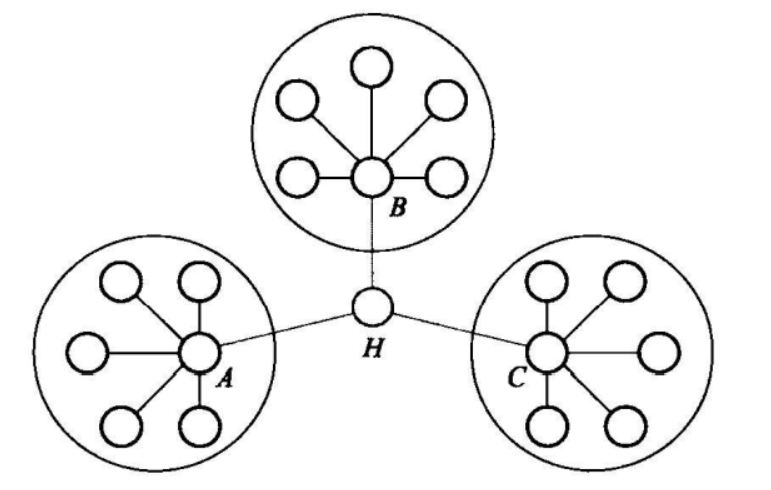
說明節點重要性的一個包含19個節點的網路

接近中心性

接近中心性（Closeness Centrality）提供一種完全不同的中心性度量方法，用於度量一個節點到其他節點的平均距離。對於網路中每一個節點，該節點到網路中所有節點的距離的平均值為，即有：

其中是節點到節點的距離。的值越小意味著節點更加接近其他節點，值的相對大小在某種程度上反映了節點在網路中的相對重要性。把的倒數定義為節點的接近中心性，接近數為：

特徵向量中心性

特徵向量中心性（Eigenvector Centrality）的基本想法是：一個節點的重要性既取決於其鄰居節點的數量（即該節點的度），也取決於其鄰居節點的重要性。記為節點的重要性度量值，則有：

其中為一比例常數，是網路的鄰接矩陣，，上式寫成矩陣形式：

上式意味著是矩陣與特徵值對應的特徵向量，疊代計算得：

k-殼與k-核

k-殼分解方法（k-shell decomposition method）是一種粗粒化的節點重要性分類方法。

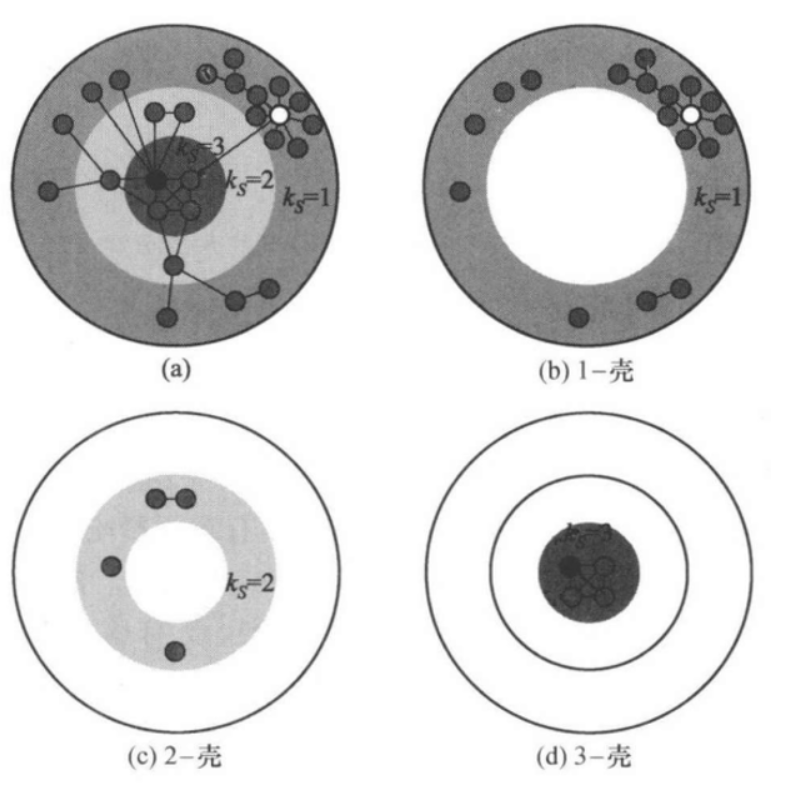
假設網路中不存在度值為 0 的孤立節點。這樣從度中心性的角度看，度為 1 的節點就是網路中最不重要的節點。如果把所有度值為 1 的節點以及與這些節點相連的邊都去掉，這時網路中可能又會出現一些新的度值為 1 的節點，再把這些節點及其相連的邊去掉，重複這種操作，直至網路中不再有度值為 1 的節點為止。這種操作形象上相當於剝去了網路的最外面一層殼，把所有這些被去除的節點以及它們之間的連邊稱為網路的 1-殼（1-shell）。有時，網路中度為 0 的孤立節點也稱為 0-殼（0-shell）。在剝去了 1-殼 後的新網路中的每個節點的度值至少為 2 。接下來可以繼續剝殼操作，即重複把網路中度值為 2 的節點及其相連的邊去掉直至不再有度值為 2 的節點為止。把這一輪所有被去除的節點及它們之間的連邊稱為網路的 2-殼（2-shell）。依次類推，可以進一步得到指標更高的殼，直至網路中的每一個節點最後都被劃分到相應的 k-殼 中，就得到了網路的 k-殼 分解。網路中的每一個節點對應於唯一的 k-殼 指標，並且-殼 中所包含的節點的度值必然滿足。

一個可以分解為三層殼的簡單網路

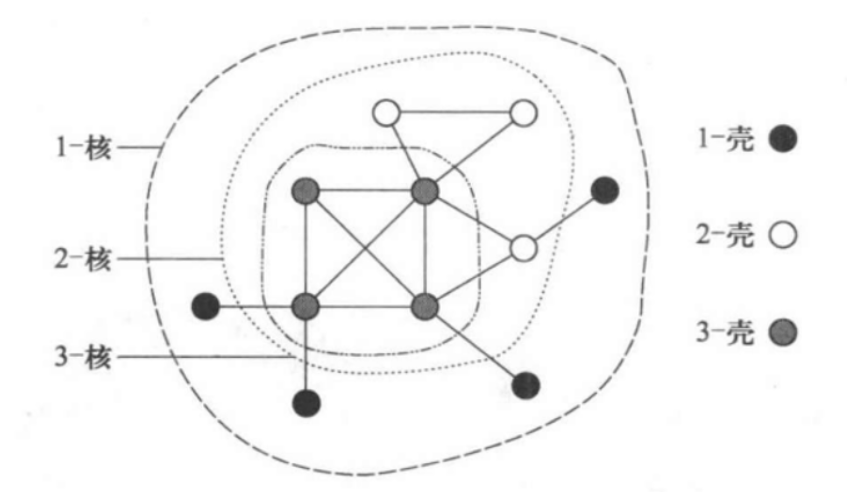
在得到一個網路的 k-殼 分解之後，把所有的 k-殼 的並集稱為網路的 k-核（k-core）把指標的 k-殼 的並集稱為網路的 k-皮（k-crust）。k-核 的一個等價定義是:它是一個網路中所有度值不小於 k 的節點組成的連通片。基於這一定義，可以按照如下方法得到 k-核：首先去除網路中度值小於 k 的所有節點及其連邊；如果在剩下的節點中仍然有度值小於 k 的節點，那么就繼續去除這些節點，直至網路中剩下的節點的度值都不小於 k 。依次取 k = 1,2,3，...，對原始網路重複這種去除操作，就得到了該網路的 k-核分解（k-core decomposition）。 對於一個連通網路，1-核 實際上就是整個網路，（k + 1）-核一定是 k-核 的子集。

一個簡單網路的k-核分解和k-殼分解

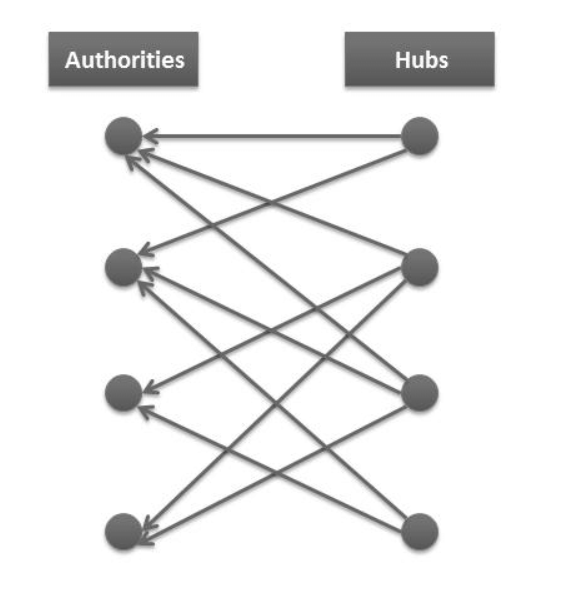
有向網路節點中心性排序算法

HITS算法

HITS算法（Hyperlink-Induced Topic Search）於1997 年由Jon Kleinberg 博士提出，是一種用於對網頁進行排序的算法。HITS算法的基本思想是：每個網頁的重要性由兩個指標刻畫，權威值（Authority）與樞紐值（Hub）。一般地，一個頁面的權威值由指向該頁面的其他頁面的樞紐值來刻畫：如果一個頁面被多個具有高樞紐值的頁面所指向，那么該頁面就具有高的權威值。另一方面，一個頁面的樞紐值由它所指向的頁面的權威值來刻畫：如果一個頁面指向多個具有高權威值的頁面，那么該頁面就具有高的樞紐值。

權威值（Authority）與樞紐值（Hub）

權威值和樞紐值是互相依存、互相影響的，它們的計算方式如下：

某網頁的權威值 = 所有指向它的網頁的樞紐值之和

某網頁的樞紐值 = 所有它指向網頁的權威值之和

在HITS算法中，每個頁面被賦予兩個屬性：Hub屬性和Authority屬性。同時，網頁被分為兩種：Hub頁面和Authority頁面。Hub頁面指那些包含了很多指向Authority頁面的連結的網頁，比如國內的一些入口網站；Authority頁面則指那些包含有實質性內容的網頁。HITS算法的目的即是通過一定的技術手段，在海量網頁中找到與用戶查詢主題相關的高質量Authority頁面和Hub頁面，尤其是Authority頁面，因為這些頁面代表了能夠滿足用戶查詢的高質量內容，搜尋引擎以此作為搜尋結果返回給用戶。

HITS算法：

（1）初始步：設定網路中所有節點的權威值和樞紐值的初始值，，。

（2）疊代過程：在第k步（k≥1）進行如下3種操作：

①權威值校正規則：每一個節點的權威值校正為指向它的節點的樞紐值之和，即

②樞紐值校正規則：每一個節點的樞紐值校正為它所指向的節點的權威值之和，即

③歸一化：

PageRank算法

PageRank算法，即網頁排名算法，於1998年由Google創始人Page和Brin提出。該算法用於對網頁進行排名，排名高的網頁表示該網頁被訪問的機率高。PageRank算法的基本思想是：網路上的一個頁面的重要性取決於指向它的其他頁面的數量和質量。

主要思想有兩點：

• 如果多個網頁指向某個網頁A，則網頁A的排名較高。

• 如果排名高A的網頁指向某個網頁B，則網頁B的排名也較高，即網頁B的排名受指向其的網頁的排名的影響。

基本的PageRank算法：

（1）初始步：給定所有節點的初始PageRank值（簡稱PR值）,,滿足

（2）基本的PageRank校正規則：把每個節點在第k-1步時的PR值平分給它所指向的節點。也就是說，如果節點的出度為，那么節點所指向的每一個節點分得的PR值為/。如果一個節點的出度為0，那么它就始終把PR值只給自己。每個節點的新的PR值校正為它所分得的PR值之和，即有

可以從網路上的隨機行走的觀點來解釋基本的PageRank算法：首先，隨機選擇一個初始節點，然後每次都從當前節點出發，從該節點指出的邊中隨機選擇一條邊並沿此邊到達另一個節點。可以證明，隨機行走步後位於節點的機率就等於基本的PageRank算法步後所得到的節點的PR值。但行走規則的缺陷在於：一旦到達某個出度為零的節點，就會永遠停留在該節點而無法再走出來。出度為零的節點也稱作懸掛節點（Dangling node），這些節點會使基本的PageRank算法失效。解決出度為零的節點問題的一種方法是給出度為零的節點賦值1/N的機率隨機訪問任意一個節點。

基本的PageRank算法的另一個問題是收斂性的問題，即便網路中沒有出度為零的節點且網路是強連通的，也會出現無法收斂的問題，比如環狀圖。解決基本的PageRank算法收斂性的有效方法是：從當前頁面出發，不管該頁面是否為出度為零的頁面，都予以一定機率隨機選取網路中任一頁面作為下一步要瀏覽的頁面。如果當前頁面的出度大於零，則以機率在當前頁面上隨機點擊某個連結而進入下一個頁面，以機率在整個網路上隨機選擇一個頁面作為下一步要瀏覽的頁面；如果當前頁面的出度為零，那么完全隨機選擇一個頁面作為下一步要瀏覽的頁面。

基於上述修正的隨機行走思想，修正的PageRank算法為：

（1）初始步：給定所有節點的初始PageRank值（簡稱PR值）,,滿足

（2）修正的PageRank校正規則：給定一個標度常數。首先按照基本的PageRank校正規則計算各個節點的PR值，然後把每個節點的PR值通過比例因子進行縮減。這樣，所有節點的PR值之和也就縮減為，再把平均分給每個節點PR值，以保持網路總的PR值為1。即有PR

關於標度常數的取值需要考慮到收斂性和有效性之間的折中：如果，那么算法會無法收斂，越接近1算法收斂速度越慢；越接近0算法收斂速度越快，如果，那么算法一步就收斂到所有節點均具有相同PR值的狀態，但收斂值缺乏有效的意義。Page和Brin當初提出PageRank算法時，建議取。