基本介紹
- 中文名:算術電路
- 外文名:arithmetic circuity
- 分類:工學
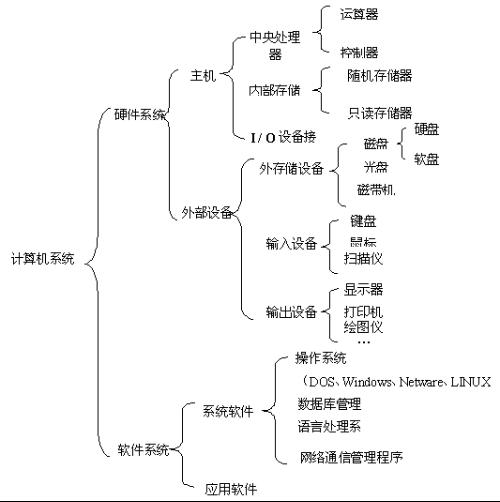
算術電路是計算機硬體中必不可少的電路,它的性能是決定計算機能力的重要因素。計算機中採用的是二進制系統,它為了能表示正、負數,必須將數冠以符號位,同時為了能用...
集成運放是一個已經裝配好的高增益直接耦合放大器,加接反饋網路以後,就組成了運算電路。...
用數位訊號完成對數字量進行算術運算和邏輯運算的電路稱為數字電路,或數字系統。由於它具有邏輯運算和邏輯處理功能,所以又稱數字邏輯電路。現代的數字電路由半導體工藝...
分析了比例係數與平衡電阻、反饋電阻的關係。目的是探索比例係數任意取值時加減法運算電路構成形式的變化。...
乘法電路(multiplying circuit)是一種完成兩個互不相關的模擬信號相乘作用的電子器件。它可以將兩個二進制數相乘。它是由更基本的加法電路組成的。...
比例運算電路,是指將輸入信號按比例放大的電路,分類有加法運算電路、減法運算電路等。...
如圖所示電路中運放的同相輸入端接信號vs,反向輸入端通過電阻 R1接地,vo與vs同相,根據“虛短”和“虛斷”vo=(1+Rf/R1)v-=(1+Rf/R1)vs故稱為同相比例...
電路計算方法是電路計算中出現較早、簡單易懂,或者使用較多、生命力較強的傳統方法。主要有表格法、支路電流法、節點電壓法和迴路電流法。...
算術邏輯單元(arithmetic and logic unit) 是能實現多組算術運算和邏輯運算的組合邏輯電路,簡稱ALU。...
數字電路能完成的算術功能有加法、減法、乘法和除法等。這與模擬電路中的比例運算、求和運算以及模擬乘法器等是不一樣的概念。模擬電路的運算完成的是對信號幅值的...
基本微分運算電路的輸出電壓對輸入電壓的變化非常敏感,所以它的抗干擾性能差,而且RC微分電路和運算放大器合在一起能夠引起自激振盪。為此可以在輸入端串聯電阻R1以...
算術控制單元,也叫控制單元(CU)是計算機的中央處理單元(CPU)的組件,其指導處理器的操作。 它告訴計算機的記憶體,算術/邏輯單元以及輸入和輸出設備如何回響程式的指令...
電路計算是國中物理電學部分中的重要內容之一.解此類計算題的方法有很多,但在解題過程中,許多同學往往找不到一種較簡單的方法,從而人為地加大解題的難度...
積分運算電路中改變電容大小使時間常數變大,上升變慢,下降也變慢,不錯,但是這不算是效果,最關鍵明顯的效果是所利用的是負指數函式曲線的前邊很小一段,因此所...
邏輯電路是一種離散信號的傳遞和處理,以二進制為原理、實現數位訊號邏輯運算和操作的電路。分組合邏輯電路和時序邏輯電路。前者由最基本的“與門”電路、“或門”...
《圖解電路計算》是2001年4月1日科學出版社出版的圖書,作者是川 毅。...... 《圖解電路計算》是2001年4月1日科學出版社出版的圖書,作者是川 毅。...
用集成運算放大器OP07和三極體8050構成對數放大電路和反對數放大電路。利用PN節的指數伏安特性實現對數反對數運算,同時用三極體代替PN節以增加集電極電流動態運用範圍。...
微分電路和積分電路的統稱。輸出電壓與輸入電壓成微分關係的電路為微分電路,通常由電容和電阻組成;輸出電壓與輸入電壓成積分關係的電路為積分電路,通常由電阻和電容...
本書被IEEE“Spectrum”雜誌稱為“電路領域的經典之作”,是歐美“電路”課程採用最為廣泛的教材。近些年國內引進了該教材,從該書的第六版開始,至今已經是第十版,...
集成運算放大電路是一種直接耦合的多級放大電路,它是利用半導體的集成工藝,實現電路、電路系統和元件三結合的產物。由於採用集成工藝,可以使相鄰元器件參數的一致性好...
《數字邏輯電路基礎》是2010年電子工業出版社出版的圖書,作者是江國強。《數字邏輯電路基礎》共10章,包括數制與編碼、邏輯代數、門電路、組合邏輯電路、觸發器、時序...
《運算放大器電路》是2009年科學出版社出版的圖書,作者是內山明治。...... 《運算放大器電路》是“電工電子技術叢書”之一。《運算放大器電路》共分7章,主要介紹...
混連電路是在一段電路中,既有串聯,也有並聯的一種混合型電路。...... 混連電路是在一段電路中,既有串聯,也有並聯的一種混合型電路。目錄 1 混聯電路 2 注意...
計數是一種最簡單基本的運算,計數器就是實現這種運算的邏輯電路,計數器在數字系統中主要是對脈衝的個數進行計數,以實現測量、計數和控制的功能,同時兼有分頻功能,...
基爾霍夫電壓定律(Kirchhoff laws)是電路中電壓所遵循的基本規律,是分析和計算較為複雜電路的基礎,1845年由德國物理學家G.R.基爾霍夫(Gustav Robert Kirchhoff,...
