正如位移/應變是結構變形的度量一樣，等效塑性應變是材料塑性變形的一個度量，等效塑性應變為一個標量，可以用於做屈服函式的內參數。
一般應變狀態下各應變分量經適當組合而形成的與單向應變等效的應變,或稱相當應變,應變強度。由於等效應變和等效應力都是將複雜應力、應變狀態等效成簡單的單向拉伸或壓縮狀態，故可用來測定複雜應力狀態下的應力—應變曲線，亦稱σe—εe為金屬材料的硬化曲線或變形抗力曲線。
基本介紹
- 中文名：等效應變
- 外文名：equivalent strain
- 學科：力學、材料學
- 別名：effective strain
- 相關名詞：等效應力、應力-應變曲線
- 功能：簡化非線性應變計算
基本介紹,相關準則,等效塑性應變,套用,
基本介紹
等效塑性應變是用來確定材料經強化後屈服面的位置的物理量，其計算公式與計算等效應力的第四強度理論計算公式是一樣的，只要把應力改成應變就成。我們在試驗中得到的是單向拉伸時材料的彈塑性應力應變曲線，而實際中結構的應力狀態往往是空間應力狀態，屈服時其也是空間屈服，通過計算等效塑性應變我們可以找到其塑性屈服後應變狀態對應的等效應力和此時結構的空間應力狀態。
等效應變的增量形式：根據列維—米澤斯(Levy-Mises)增量理論(見塑性增量理論)dεij=dλσij,代入dεe式中,可得到等效應力。等效是把一維的拉壓試驗結果推廣到三維的一種手段，取決於你用哪種等效，如果你用von-Mises準則，那么等效應變 = (2/9 *[（Exx-Eyy）^2+ （Eyy-Ezz）^2+（Exx-Ezz）^2+6*（Exy^2+Eyz^2+Exz^2）])^(1/2)其中E是應變，ij是下標。
在小變形時,應力應變的定義是唯一的,但在有限變形時則是多種多樣的,一般認為,在本構關係中選用什麼應力應變對都是可以的,但在塑性理論中,由於等效應力、等效應變的採用,所以應力應變並不可以任意選擇,也就是說,並不是對所有的應力應變對等效應力、等效應變的思想都成立。
相關準則
米塞斯（Von.Mises）屈服準則
1.米塞斯屈服準則的數學表達式在一定的變形條件下，當受力物體內一點的應力偏張力的第二不變數
J2'達到某一定值時，該點就開始進入塑性狀態。即
用主應力表示為
式中σs——材料的屈服點K——材料的剪下屈服強度
與等效應力比較，可得
所以，米塞斯屈服準則也可以表述為：在一定的變形條件下，當受力物體內一點的等效應力達到某一定值時，該點就開始進入塑性狀態。
等效塑性應變
等效塑形應變是用來確定材料經強化後屈服面的位置的物理量，其計算公式與計算等效應力的第四強度理論計算公式是一樣的，只要把應力改成應變就成。我們在試驗中得到的是單向拉伸時材料的彈塑性應力應變曲線，而實際中結構的應力狀態往往是空間應力狀態，屈服時其也是空間屈服，通過計算等效塑形應變我們可以找到其塑性屈服後應變狀態對應的等效應力和此時結構的空間應力狀態。
套用
將複雜的多軸應力-應變關係轉化為單軸簡單應力-應變關係，採用等效應力或等效應變概念來研究材料模型是近年來國內外的研究趨勢。
Darwin和Pecknold在1977年首次給出了增量型等效單軸應變方法，Mazars在混凝土多軸損傷研究中，也引進等效應變的概念，但給出的損傷模型是建立在混凝土為各向同性材料的假設基礎之上。
韋未、李同春提出了一種可以適用複雜空間應力狀態的四參數等效應變損傷模型，主要適用於各向同性混凝土材料峰值前的彈性階段，不能全面反映混凝土應力-應變關係曲線全過程損傷特性。
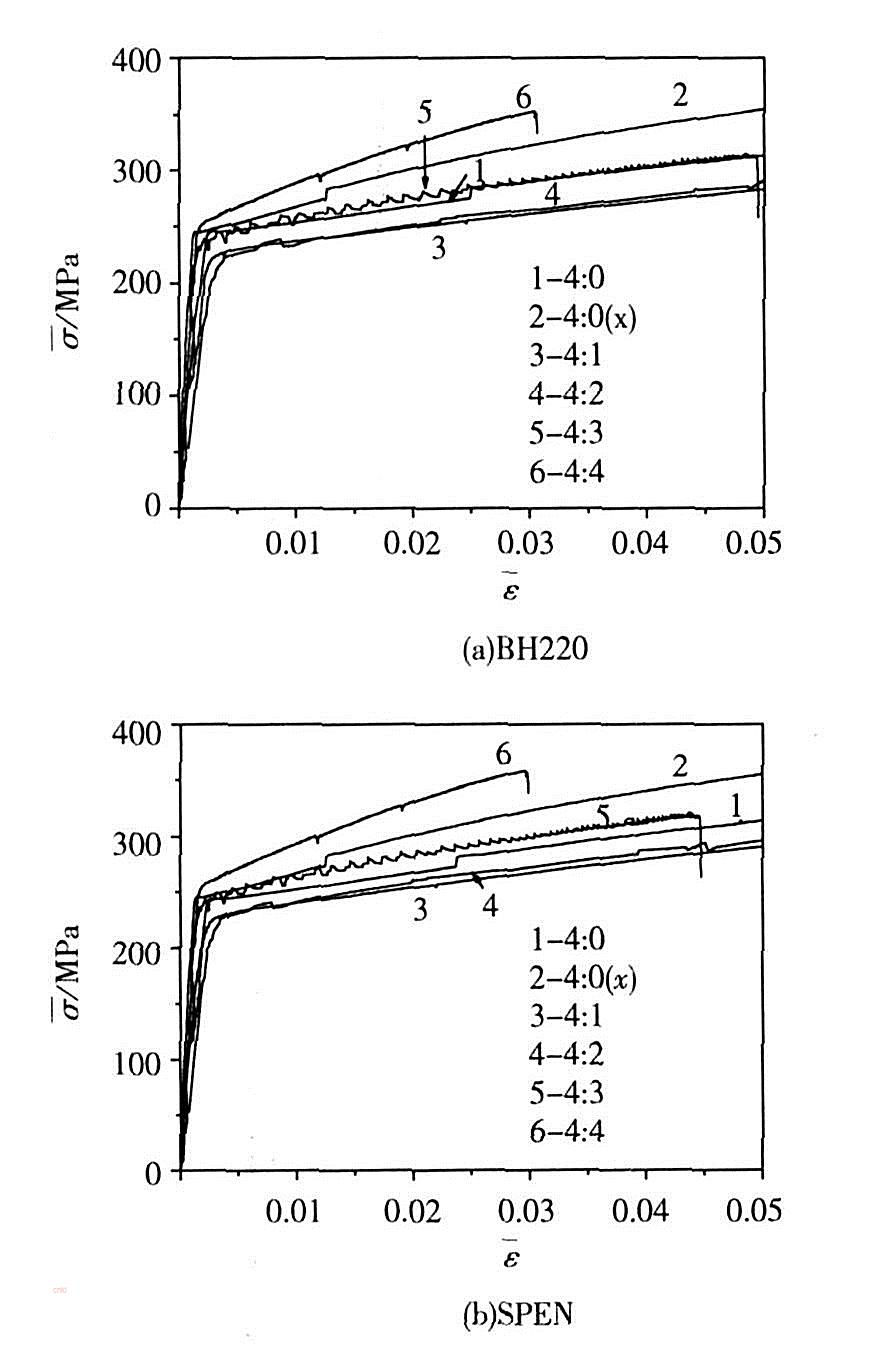
吳向東、萬敏等為研究不同屈服準則下板材等效應力-等效應變曲線的適用性，基於Hill48、Hill79、Hill90和Hosford屈服準則和試驗獲得的板材雙向拉伸應力應變曲線（如右圖），對兩種薄鋼板在不同載入比例下的等效應力-等效應變曲線進行了試驗研究和理論分析。
楊俊等人針對輪盤低循環疲勞載荷非對稱及其主要壽命區限,提出一種簡化的等效應變壽命預測模型,對某型發動機高壓壓氣機I級盤進行了低循環疲勞壽命預測。通過與試驗壽命的比較,等效應變壽命預測誤差為41.8%,Manson-Coffin預測誤差為99.2%。結果表明:簡化的等效應變壽命預測方法是有效的,而且對試驗盤的壽命預測精度比Manson-Coffin預測模型高。
