萬有引力、電磁力、弱力、強力的統一是物理領域研究的重心之一，目前世界上還沒有任何一種理論能夠實現四力統一，“四力統一”涉及到空間的最基本存在形式以及物質創生與分化等大量問題。
等價場力學的創新點主要有3個：（1）用“場內斂”這一概念來做為物質熱吸收的起源，用“場內斂”與“場內斂平衡”這兩個概念來統一四力的起源問題，“場內斂”為物質間“場相互作用”的一種機制，“場內斂率”能夠貫通物質引力、電磁力、弱力、強力4種力學特徵的變化；（2）提出自然界物質系“廣泛性存在規律”的“靜態場內斂率對應性關聯方程”（不含光子），該方程只需知道客體對主體的環繞周期與環繞半徑無需知道“環繞客體”的質量值就可精確計算出主體的質量值；（3）依據“靜態場內斂率對應性關聯方程”提出“飽和態場內斂”的概念，進而提出空間為一個基於“靜態場內斂率對應性關聯方程”呈體系性“飽和場平衡”的概念，從這裡可推導出特定空間對其特定“場內斂率值”的守衡，進一步可推導出任意空間“場內斂率值守衡張量”的存在，“空間SH值守衡張量”對外來物質有斥力作用而對系內物質的“場內斂率升值行為”有一定的阻遏力。
基本介紹
- 中文名：等價場力學基本原理
- 外文名：Basic Principle of Equivalent Field Mechanics
關鍵字：等價場；場內斂；場內斂平衡；場內斂率S；場失衡能QE；飽和態場平衡；電子勢能阱；場禁止的雙向性；場慣勢；
一：等價場原理
一：等價場原理
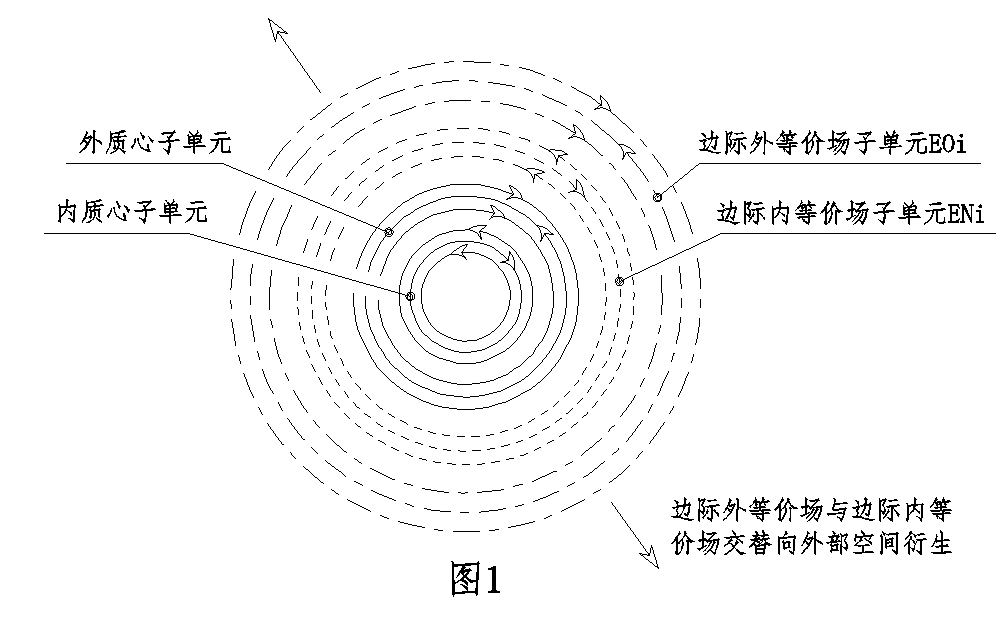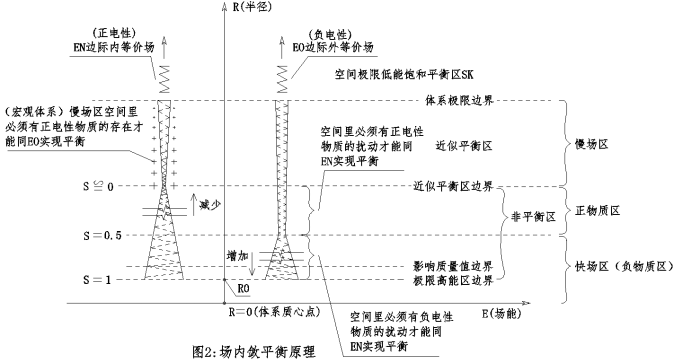
等價場原理理論假設：任何物質體在其外圍存在一個與“自體實體”的質能值相等的“等價場體系”，等價場體系由邊際內等價場體系(EN)與邊際外等價場體系(EO)構成且各自的總場能值相等即EN=EO，EN與EO有各自的子單元構成、其子單元交替向外部空間衍生，EN與EO相鄰的“一對子單元構成”稱為ENi與EOi，ENi與EOi的磁場流分布規律為反對稱的關係（圖1），以整體來看EO體系位於EN體系的外部、空間的位置關係使ENi磁場能量的密度以極微小的程度大於EOi，等價場體系在其存在範圍內系統性的受到空間裡“磁波”的擾動進而發生場內斂，子單元ENi與EOi“場能量密度”的差異性導致兩者被空間磁波所消弱的程度不同，這種差異性使EN與EO各自場內斂的程度也不相同、EN內斂的程度大而EO內斂的程度輕，等價場這種內斂效應的偏置性最終積累於一個體系的近距空間（圖2）,物質近程上的場內斂區由廣域空間的系統性所賦予、這種系統性為極大尺度里的事件，特定空間場失衡的程度用場內斂率S來表示，空間磁波相互作用產生的能量對於物質以自體場內斂率S增加的方式來體現，場內斂率S值決定物質體運動屬性以及其空間場失衡的分布特徵。
場內斂的本質是空間磁波相互間存在擾動產生自然做功進而將能量傳導到體系的近區空間、場內斂的能量以一種非平衡的方式存在，熱吸收是廣域空間磁場做功的結果，熱輻射是體系“場內斂平衡”的結果，粒子熱吸收與其熱輻射的能力是平衡的關係，粒子熱吸收能力與其場內斂率S間存在特定的關聯關係，“飽和空間系統”有物質進入後引發“場內斂平衡”的失衡、空間磁波是“飽和空間系統”場內斂平衡的結果。一個體系磁波的波動特徵在空間的分布有其規律性，在穩定的飽和態條件下一個定域空間在一定時間內所經過的能量越多、在此區域裡“場平衡行為”所造成的磁波波動頻率就越大，這一分布規律用場內斂率S也可精確描述。物質相互間存在的“場擾動作用”使一個系統內任何對象的“場內斂率值”均都有所增加，“場內斂”為一種物質間相互影響的機制。
二：場內斂平衡原理
場內斂的本質是空間磁波相互間存在擾動產生自然做功進而將能量傳導到體系的近區空間、場內斂的能量以一種非平衡的方式存在，熱吸收是廣域空間磁場做功的結果，熱輻射是體系“場內斂平衡”的結果，粒子熱吸收與其熱輻射的能力是平衡的關係，粒子熱吸收能力與其場內斂率S間存在特定的關聯關係，“飽和空間系統”有物質進入後引發“場內斂平衡”的失衡、空間磁波是“飽和空間系統”場內斂平衡的結果。一個體系磁波的波動特徵在空間的分布有其規律性，在穩定的飽和態條件下一個定域空間在一定時間內所經過的能量越多、在此區域裡“場平衡行為”所造成的磁波波動頻率就越大，這一分布規律用場內斂率S也可精確描述。物質相互間存在的“場擾動作用”使一個系統內任何對象的“場內斂率值”均都有所增加，“場內斂”為一種物質間相互影響的機制。
二：場內斂平衡原理
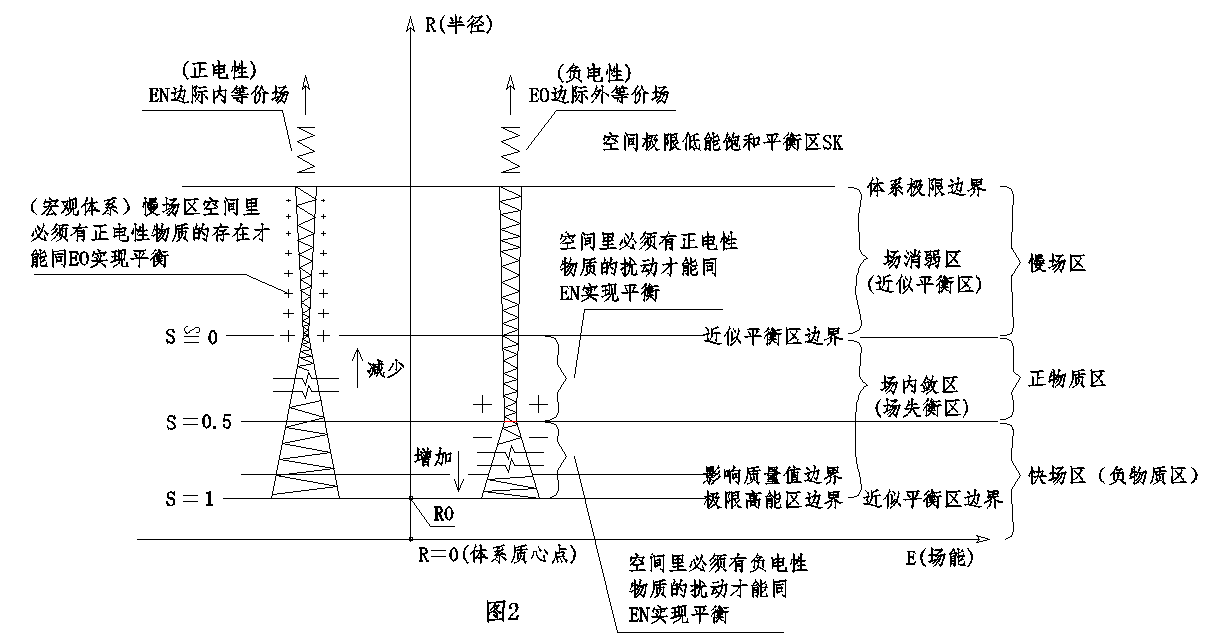場內斂平衡原理物質體系場內斂造成其近區空間的場失衡，場失衡需要特定物質對所在空間的邊際內等價場進行擾動以使其場內斂的程度與邊際外等價場達到平衡,“場平衡施體”的擾動行為對邊際外等價場有增加其內斂的作用、而對邊際內等價場有減少其場內斂的作用（圖2），物質存在是空間“場內斂失衡”的產物，巨觀系統場內斂平衡原則：一個巨觀系統在“場內斂區”之外的慢場區空間裡所存在的“正電性慢物質的總質能值”等於慢場區空間裡邊際內等價場體系與邊際外等價場體系兩者的總場能值之差（應當考慮系內所存在的運動態光子的擾動效能），在一個體系內物質間既是“相互擾體”的關係也是“相互場平衡施體”的關係，Si=Sh條件下物質體的運動屬性由所在空間的場失衡特性所賦予。物質粒子以運動來做為空間“等價場系統”實現場平衡的唯一方式決定了空間不能夠實現絕對的場平衡，“場內斂”在來源上如果具備連續性存在那么“場平衡”也必須具備恆定存在。量子糾纏的超距作用反央出物質間的關係在本質上不是點對點的關係、而是場與場相互間系統性關聯的關係，這種關聯基於相互間互為“場平衡施體”的關係。
“等價場力學”用“靜態場內斂率對應性關聯方程”來描述廣域概念“物質系統”場失衡性在空間的分布規律（不含光子），用物質自體的場內斂率S來描述其空間場失衡性的特定分布特徵，物質在特定空間的運動屬性用其自體的S值和其存在空間的場內斂率Sh值來描述，物質間的所有力學關係統一在“場內斂平衡”這一機制下去描述。
物質體外部空間磁場強度的改變能夠影響其自體的場內斂率S，除去標準光速外同一速度對一個體系的邊際外等價場與邊際內等價場的影響不同，物質體“場平衡效率”隨其速度或其場內斂率S的增加而增加，“場平衡效率”的增加使物質體外“場失衡性的場內斂區”以一定程度減小，當自體場內斂率S=0.5時物質在其空間的S0.5區以外實現極高程度的場平衡、即在S<0.5區域實現∑ENi=∑EOi，當物質體S大於0.5後其“場內斂區”幾乎消失、但“場內斂區”外部的“慢場區空間”卻隨之增大、同時慢場區“場失衡性”的程度也隨之相應增大，慢場區在其主體S<0.5時的特點是“場失衡性”極微弱。
物質體外部空間磁場強度的改變能夠影響其自體的場內斂率S，除去標準光速外同一速度對一個體系的邊際外等價場與邊際內等價場的影響不同，物質體“場平衡效率”隨其速度或其場內斂率S的增加而增加，“場平衡效率”的增加使物質體外“場失衡性的場內斂區”以一定程度減小，當自體場內斂率S=0.5時物質在其空間的S0.5區以外實現極高程度的場平衡、即在S<0.5區域實現∑ENi=∑EOi，當物質體S大於0.5後其“場內斂區”幾乎消失、但“場內斂區”外部的“慢場區空間”卻隨之增大、同時慢場區“場失衡性”的程度也隨之相應增大，慢場區在其主體S<0.5時的特點是“場失衡性”極微弱。
空間磁場對物質有“等效用”的場擾作用和場平衡作用，以太陽係為例：行星距離太陽越近其外圍場失衡的程度越小，近距行星因外空間處於場平衡態造成衛星不能夠穩定存在（無需衛星存在），太陽系遠距行星需要更多的衛星才能夠實現其外空間的場平衡，物質的場擾作用與場平衡作用最終只能是以物質外部的等價場來實現。
邊際外等價場EO與邊際內等價場EN是相互平衡、相互制約的關聯關係，平衡性場行為在通過EO與EN時對兩者都有內斂作用，在場內斂區內同一個場擾動條件下EN內斂程度只有EO的0.604897432倍，也就是說場平衡行為每完成1份場平衡效用另產生出0.604897432份失衡性，一個質子如果讓其等價場的失衡性完全不存在其質量就要增加5.061976698倍電子的質量值。
MP=MO+Me▪Si[1+0.604897432(1+2∧2+3∧3...N∧N)]
(MP為質子的動態質量值，MO為質子Si≌0時的質量值，Me為電子的質量值，Si為質子動態的場內斂率值)
三：飽和態場平衡與局部型場平衡
“飽和態場平衡”的定義：物質“等價場體系”全範圍完整實現與“存在環境Sh”真正對等的場平衡。“飽和態場平衡”需要對象物質體在“特定值的Sh環境”里穩定存在極長時間才能夠實現。“飽和態場平衡”的對象物質其“場內斂率S值”的改變是一個極其緩慢的過程，物質體在近距上以快速方式所實現的場內斂率增加為“局部型場平衡”，“局部型場平衡”產生的能量會被該體系“飽和態場平衡”的能量逐步稀釋掉，局部型“場內斂率S值”的衰退時間與其形成時間存在關聯關係，劇烈的場內斂率增加能夠一定程度上增加體系中“主體實體”的質量值，物質實體質量的衰減速度取決於該體系中所含“局部型場內斂”的成份。
“飽和態場平衡”的定義：物質“等價場體系”全範圍完整實現與“存在環境Sh”真正對等的場平衡。“飽和態場平衡”需要對象物質體在“特定值的Sh環境”里穩定存在極長時間才能夠實現。“飽和態場平衡”的對象物質其“場內斂率S值”的改變是一個極其緩慢的過程，物質體在近距上以快速方式所實現的場內斂率增加為“局部型場平衡”，“局部型場平衡”產生的能量會被該體系“飽和態場平衡”的能量逐步稀釋掉，局部型“場內斂率S值”的衰退時間與其形成時間存在關聯關係，劇烈的場內斂率增加能夠一定程度上增加體系中“主體實體”的質量值，物質實體質量的衰減速度取決於該體系中所含“局部型場內斂”的成份。
四：場失衡能QE
場失衡能QE是指一個對象物質其“等價場系統”中所存在的“場內斂性失衡能的總值”，“場失衡能QE”在概念上不同於量子力學中的E=hv，E=hv是特定光子對物質或空間的擾動能力所產生出的等價能的描述，正電性對空間的擾動能力與其電荷量間的關係是倍比關係、而負電荷則是某種指數關係（註：精確公式作者尚未找到），E=hv是光子負電荷達到“特定臨界值”後、光子“負電性成分”在與空間互動作用過程中所產生出的熱吸收與熱輻射能力的反央，正電性的“場內斂區”相對縮小能夠強化物質正電荷對空間的擾動能力，物質在S≌0.5時對空間的擾動能力最小，因為S≌0.5時粒子“失衡性的場內斂區”幾近消失、且整個體系處於最理想的場平衡態。電子對質子的逃逸動能由質子場失衡能QE的減少所賦予。
場失衡能QE是指一個對象物質其“等價場系統”中所存在的“場內斂性失衡能的總值”，“場失衡能QE”在概念上不同於量子力學中的E=hv，E=hv是特定光子對物質或空間的擾動能力所產生出的等價能的描述，正電性對空間的擾動能力與其電荷量間的關係是倍比關係、而負電荷則是某種指數關係（註：精確公式作者尚未找到），E=hv是光子負電荷達到“特定臨界值”後、光子“負電性成分”在與空間互動作用過程中所產生出的熱吸收與熱輻射能力的反央，正電性的“場內斂區”相對縮小能夠強化物質正電荷對空間的擾動能力，物質在S≌0.5時對空間的擾動能力最小，因為S≌0.5時粒子“失衡性的場內斂區”幾近消失、且整個體系處於最理想的場平衡態。電子對質子的逃逸動能由質子場失衡能QE的減少所賦予。
QEi=EOi-ENi；（QEi為物質等價場體系“一對相鄰子單元”的場失衡能,一個體系慢場區“等價場”的QEi為正值、SK≤Si≤1近程區域上“等價場”的QEi為負值，正物質近程上SK≤Si≤1區域“等價場”的QEi為負值，負物質近程上SK≤Si≤1區域“等價場”的QEi為正值）
QE=∑QEi；（在粒子等價場空間S=0至S=1區間）
QE=（1-2Si）limQE（limQE為一個體系存在的最大值場失衡能，Si為該物質體系的飽和態場內斂率，粒子Si≌0時其等價場在近程上帶有正最大值的場失衡能，粒子Si=1時其等價場在遠程上的大範圍空間裡系統性帶有負最大值的場失衡能。）
Si≥0.5的粒子離開“等價存在環境Sh”後從其“等價場系負電荷”與空間的作用中獲得動力，物質Si值如大於所在空間的Sh值就會受到空間裡排斥性的“Sh值守衡張量力”，外在因素在短期內並不能夠改變物質的飽和態場內斂率，“Sh值守衡張量”能夠使空間始終以場平衡的方式存在，正電性在近程上以“能量的相對集中存在”來反央，負電性以“能量大範圍系統性分散存在的方式”來反央。
QE=（1-2Si）limQE（limQE為一個體系存在的最大值場失衡能，Si為該物質體系的飽和態場內斂率，粒子Si≌0時其等價場在近程上帶有正最大值的場失衡能，粒子Si=1時其等價場在遠程上的大範圍空間裡系統性帶有負最大值的場失衡能。）
Si≥0.5的粒子離開“等價存在環境Sh”後從其“等價場系負電荷”與空間的作用中獲得動力，物質Si值如大於所在空間的Sh值就會受到空間裡排斥性的“Sh值守衡張量力”，外在因素在短期內並不能夠改變物質的飽和態場內斂率，“Sh值守衡張量”能夠使空間始終以場平衡的方式存在，正電性在近程上以“能量的相對集中存在”來反央，負電性以“能量大範圍系統性分散存在的方式”來反央。
五：電子勢能阱
質子場內斂失衡最大的區域（S0.5區域附屬檔案）為“電子勢能阱”，“電子勢能阱”是電子創生的環境，電子對質子的逃逸能量由質子總體的場失衡能QE減少所賦予，質子的場內斂率從S≌0→S=0.5發展時、場內斂失衡區向質子中心區壓縮、場能量也向質子中心區匯聚（因電子逃逸後失衡區的場平衡有場能量替代），質子S≌1時質子場內斂失衡的能量與場內斂平衡的能量兩者全部轉換成質量，在質子場內斂率由S≌1→S≌0發展時、場內斂失衡區外移、同時場內斂平衡的場能量也向質子外圍擴散、高能區的場平衡能量經過S0.5區時被“電子勢能阱”整合為“電子”。
六：場內斂平衡方程
物質體自體的場內斂率用S表示，物質體存在空間的場內斂率用Sh表示。
（1）Sk≤S≤1(Sk為自然界空間所存在的極限最低場內斂率。)
（2）Si=Sh(Si=Sh為飽和態場平衡關係下物質體與存在環境間的對等關係式。)
物質體自體的場內斂率用S表示，物質體存在空間的場內斂率用Sh表示。
（1）Sk≤S≤1(Sk為自然界空間所存在的極限最低場內斂率。)
（2）Si=Sh(Si=Sh為飽和態場平衡關係下物質體與存在環境間的對等關係式。)
（3）Vi=Si×2C；Si=Sh；Sh≤0.5；(Si為對象體系的飽和態場內斂率值，Sh為對象體系所在環境的飽和態場內斂率值；C為光速，Vi為對象體的向心環繞速度其大小由所在環境的場失衡程度所賦予，場失衡程度最大的空間其粒子的運動速度為光速。）
（4）Vi=SN×2C；SN>Sh；Sh≤0.5；（SN為對象體系局部型或者飽和態的場內斂率值，Sh為對象體系所在環境的飽和態場內斂率值。）
（5）Vi=C；1≥Si≥0.5；Sh≤0.5；（Sh為粒子存在環境的飽和態場內斂率，Vi為粒子的運動速度，Si為粒子的飽和態場內斂率，C為光速；）
（6）Vi=（1-Si）×2C；1≥Si≥0.5，Si=Sh，（C為光速。）
（5）Vi=C；1≥Si≥0.5；Sh≤0.5；（Sh為粒子存在環境的飽和態場內斂率，Vi為粒子的運動速度，Si為粒子的飽和態場內斂率，C為光速；）
（6）Vi=（1-Si）×2C；1≥Si≥0.5，Si=Sh，（C為光速。）
七：靜態場內斂率對應性關聯方程（場平衡效率方程）
一個體系內的兩個物質單元具有同一恆定值的飽和態場內斂率、如果質量都一定值增加，在沒有外在場平衡約束的條件下，做為相互的場平衡施體、兩者的場平衡效率必須有所下降、也就是說兩者間的距離必然增加，這一推論違背牛頓的萬有引力公式，由這一結果可推導出物質體系間的距離關係由物質體系固有的飽和態場內斂率所賦予。
太陽系各天體的RO值（表一） | |||||
平均公轉速度（KM/秒） | 公轉周期（天） | 軌道半長軸（KM） | 各行星計算出的太陽RO值（KM） | 各行星的RO值 （KM） | |
太陽 | 220.00 | ||||
水星 | 47.50035043 | 87.96908 | 57909050.0 | 1.886584946 | |
金星 | 35.02006027 | 224.701 | 108208000.0 | 1.908727573 | |
地球 | 29.78381512 | 365.24219 | 149587443.7 | 1.908653403 | 0.001057109 |
火星 | 24.08920653 | 686.98 | 227925000.0 | 1.904021729 | 0.000331074 |
木星 | 13.07331264 | 4328.9 | 778547200.0 | 1.910879751 | 0.018773829 |
土星 | 9.689627661 | 10752.17 | 1433449369.5 | 1.92165228 | 0.010296588 |
天王星 | 6.794558624 | 30778.01399 | 2876679082.5 | 1.909098263 | 0.004019555 |
海王星 | 5.444410512 | 60152.0 | 4503443661.5 | 1.914332809 | 0.004358451 |
M0=4π/3(RO∧3)K(M0為一個物質體系實體的質量值，RO為該物質體系的常數半徑，K為常數)
光子在自然界裡沒有合適的場平衡施體存在、其“場內斂”不能夠最終演化成Si=RO/√Ri平方反比分布規律，光子“等價場系空間”不存在大值QE的區域，光子的場失衡能QE以極微弱、相對勻化、大範圍分布為特徵，這種特徵使光子“飽和態場內斂率值”改變所需的時間更長，光子相互間所具有的“遠距糾纏能力”與光子場能量的大範圍分布特徵有關。
八：靜止質量
（1）物質的“動能質量”VM公式：
VM=M0×Si；（M0為一個物質實體的質量值，Si為該體系的飽和態場內斂率；）
（2）物質的“阻動質量”FM公式：FM=M0(1－Si)；
（3）：“靜止質量”M公式：
M=（FM－VM）=>M=M0(1-2Si)；
當物質Si∑EOi）；當物質Si=0.5時成為電中性物質；當物質Si>0.5時成為負質量物質；當物質Si≥0.5、存在環境的Sh≤0.5時其在近程上表現為電中性，而在遠程上（慢場區）表現為極微弱、相對勻化、大範圍分布的負電性（即慢場區由近似平衡態變為相對較明顯的∑EOi>∑ENi）、並且其靜止質量為零值。
八：靜止質量
（1）物質的“動能質量”VM公式：
VM=M0×Si；（M0為一個物質實體的質量值，Si為該體系的飽和態場內斂率；）
（2）物質的“阻動質量”FM公式：FM=M0(1－Si)；
（3）：“靜止質量”M公式：
M=（FM－VM）=>M=M0(1-2Si)；
當物質Si∑EOi）；當物質Si=0.5時成為電中性物質；當物質Si>0.5時成為負質量物質；當物質Si≥0.5、存在環境的Sh≤0.5時其在近程上表現為電中性，而在遠程上（慢場區）表現為極微弱、相對勻化、大範圍分布的負電性（即慢場區由近似平衡態變為相對較明顯的∑EOi>∑ENi）、並且其靜止質量為零值。
一對反物質
Si從0至0.5區的質子帶正電荷其電子帶負電荷（電子Si>0.5），Si大於0.5的質子帶負電荷其電子帶正電荷（電子Si<0.5）、但條件是質子的Si值必須在S0.5上下的近區，物質系間引力或斥力的力學關係用物質自體的場內斂率S和物質存在空間的場內斂率Sh來描述。
limF=M0·△S·g(limF為物質間的最大引力，M0為該粒子的質量值，△S為物質進入一個系統處於穩定態後所增加的場內斂率，g為常數。）
九：力程方程
L=（RO∧2）/（Si∧2）；Si=Sh；（L為粒子的力程，R0∧2為一個粒子“場內斂率”等於1區域的半徑，Si為該體系的“飽和態場內斂率”，Si≥0.5的粒子在Si=Sh的環境裡其力程隨Si的增加而減小。）
九：力程方程
L=（RO∧2）/（Si∧2）；Si=Sh；（L為粒子的力程，R0∧2為一個粒子“場內斂率”等於1區域的半徑，Si為該體系的“飽和態場內斂率”，Si≥0.5的粒子在Si=Sh的環境裡其力程隨Si的增加而減小。）
十：場禁止的雙向性、場分離
一個體系內物質間的關係既是“相互擾體”的關係又是“相互場平衡施體”的關係，“場平衡施體”與主體粒子間存在“雙向場內斂效應”，自然界質量最小的粒子或者近程上不能夠存在“場平衡施體”的粒子其“場內斂率S值”有機會達到自然界“場內斂率的極限最小值SK”，粒子場內斂的能力與其質量值成正比、可以推導出光子的場失衡能只能以“相對系統性分散的方式存在”而不能夠演化為“在近程上以相對集中的方式存在”，大質量粒子因“場平衡施體”對其“等價場體系”的擾動作用其“場內斂率S的極限最小值”相對要大的多，大質量“主體粒子”的運動速度受制於其“場平衡施體”對其所帶“電荷能”的禁止作用。“高S值粒子”的場能量會被系內“場內斂的能量系”所禁止，禁止的結果造成粒子等價場與其實體的分離，場分離是造成粒子量子糾纏態的根源之一。
十一：輻射光子與其主體場內斂率的關係
Sp=Si(Sp為輻射光子的場內斂率，Si為輻射粒子的場內斂率；)
十一：輻射光子與其主體場內斂率的關係
Sp=Si(Sp為輻射光子的場內斂率，Si為輻射粒子的場內斂率；)
十二：慢場區的手征性
Si小於0.5的粒子與Si大於0.5的粒子相比較其“手征性的規律相反”，巨觀體系其空間Si≌0的廣大區域為“慢場區”，巨觀體系“慢場區”的“巨觀系手征性”與“微觀粒子Si值”大於0.5的粒子相同,巨觀天體外圍的“慢場區”有數量龐大的Si值近似等於0的“慢物質”構成，“慢場區”大量“慢物質”的存在是一個體系“場平衡”的需要。
十三：場內斂率S的波動性特徵
Si小於0.5的粒子與Si大於0.5的粒子相比較其“手征性的規律相反”，巨觀體系其空間Si≌0的廣大區域為“慢場區”，巨觀體系“慢場區”的“巨觀系手征性”與“微觀粒子Si值”大於0.5的粒子相同,巨觀天體外圍的“慢場區”有數量龐大的Si值近似等於0的“慢物質”構成，“慢場區”大量“慢物質”的存在是一個體系“場平衡”的需要。
十三：場內斂率S的波動性特徵
主體粒子“場失衡性”在空間的分布規律由所在空間（包含廣域概念的空間）總體的磁波擾動規律所支配，“場平衡機制”需要一個傳導過程、期間粒子在廣域空間所受到的“場擾動”能增加粒子的S值，場平衡機制的傳導過程造成粒子“場內斂S值”的波動，“場平衡施體”距離“主體粒子”越近其S值的波動幅度越小。
十四：場慣勢
物質的運動屬性（速度、自旋與軸傾斜）由空間的“場擾動因素”所造成，在“飽和空間系統里”任何“場擾動因素”以空間場內斂率的變化來反央，將“物質場擾動因素”在空間所產生的能量稱為“場擾能”，“場擾能”存在“外延”與“內延”兩種傳導方式，外延：在空間“Sh值守衡張量”的平衡下“場擾能”趨於向“事件點”的外部空間傳導、並實現逐步消弱，內延:“場擾效應”在“場內斂”機制下向“主體質心區”的最內部傳導，物質外在的等價場來源於物質的質心體，物質的“動能信息”在源頭上存儲於其“質心體”，物質的“動能”依靠其“等價場”與空間中場的相互作用來實現，物質的“等價場系”與其“質心體”是“統一體”的關係，低S值的物質處在相對高的Sh環境裡時其外部空間的“場擾能信息”在“質心區”逐步由外向記憶體儲、同時其“等價場系統”由內向外調整能量信息，當飽和態的高S值物質進人“低能環境”時其“等價場系”與“質心體”所存儲的能量信息就會按照存儲時的相反時間順序逐步釋放，物質“質心區”的能量信息存儲用“飽和態場內斂機制”來描述，將物質“場擾能信息”的存儲與釋放機制稱為“場慣勢”，“場慣勢”是物質慣性的來源。
論文結論：
（1）物質間的引力除了與質量值、相互間的距離大小有關外還與各自的內在屬性（S值）和存在環境的（Sh值）有關聯。（2）巨觀體系中天體的動能演化由體系整體的場內斂平衡被破壞所賦予，在體系場平衡態不被任何改變的前提下一個物質體系內主體與各場平衡施體的質量值與能態會被鎖定。（3）天體在低S值的環境裡不會形成黑洞，在宇宙的最極限條件下（Sh=1）任何粒子以場能的方式存在。（4）空間只要存在失衡性就必然存在物質（運動態或相對靜止態的物質），宇宙的起源與演化以“等價場力學”的飽和時空觀來衡量:星系體系的演化不可能存在突變，“星系體系”過於龐大時超大型星系間的空檔區也會越大，這些空檔區足夠大時在場內斂機制下會形成新的星系，空檔區新星系的發展會對大型星系的大型化發展形成制約，宇宙演化是在向大型化和小型化兩個方向演化。
引文：
【1】王明理.場內斂平衡方程組[J].科技視界，2015(27):341-344
【2】美國俄亥俄州的IMB探測器（theIrvine-Michigan-Brookhavendetector）關於質子衰變研究公布的數據。
【3】日本超級神岡探測器關於質子衰變研究公布的數據。
【4】歐洲大型強子對撞機(LargeHadronCollider)高能對撞中新生粒子質量衰減公布的數據。
