基本介紹
概念,特點,運用及意義,
概念
在重力場中,任一物體在某高度上所具有的位能稱為重力位勢,簡稱位勢,用Ф表示。位勢相等的面為等位勢面,在此面上移動時,重力所作的功等於零。而從一個等位勢面向上移動到另一個等位勢面時,就必須抵抗重力而作功,其大小等於兩處位勢值之差。在氣象學上廣泛套用位勢高度來代替幾何高度。
特點
由流速場與速度勢的關係V=Vφ可知,流速矢與等位勢面相垂直,由高位勢流向低位勢,等位勢面緊密處,位勢梯度大,相應的流速大;等位勢面稀疏處,位勢梯度小,相應的流速小,由此可見用速度勢描述無旋運動的方便之處。
Φ=常數的面稱為等位勢面。顯然海平面是Φ=0的等位勢面。等位勢面有兩個值得注意的特點:
①重力垂直於等位勢面。
若物體在空間位移ds,ds與g之間的夾角為θ,則
dΦ=gdscosθ
如ds在等θ面上,則dΦ=0,故gdscosθ=0,但g不等於0,ds不等於0,故只能是cosθ=0,θ=π/2.
這就是說ds與g垂直,而ds是位於等Φ面上的,所以等Φ面也同g垂直。
等位勢面的這一性質,使得以等位勢面作參考面有很大的優點。以等高面作參考面時,因為重力不垂直於等高面,重力在等高面內就存在分力。要是以等位勢面作參考面,就不會有在等位勢面內的重力分力。
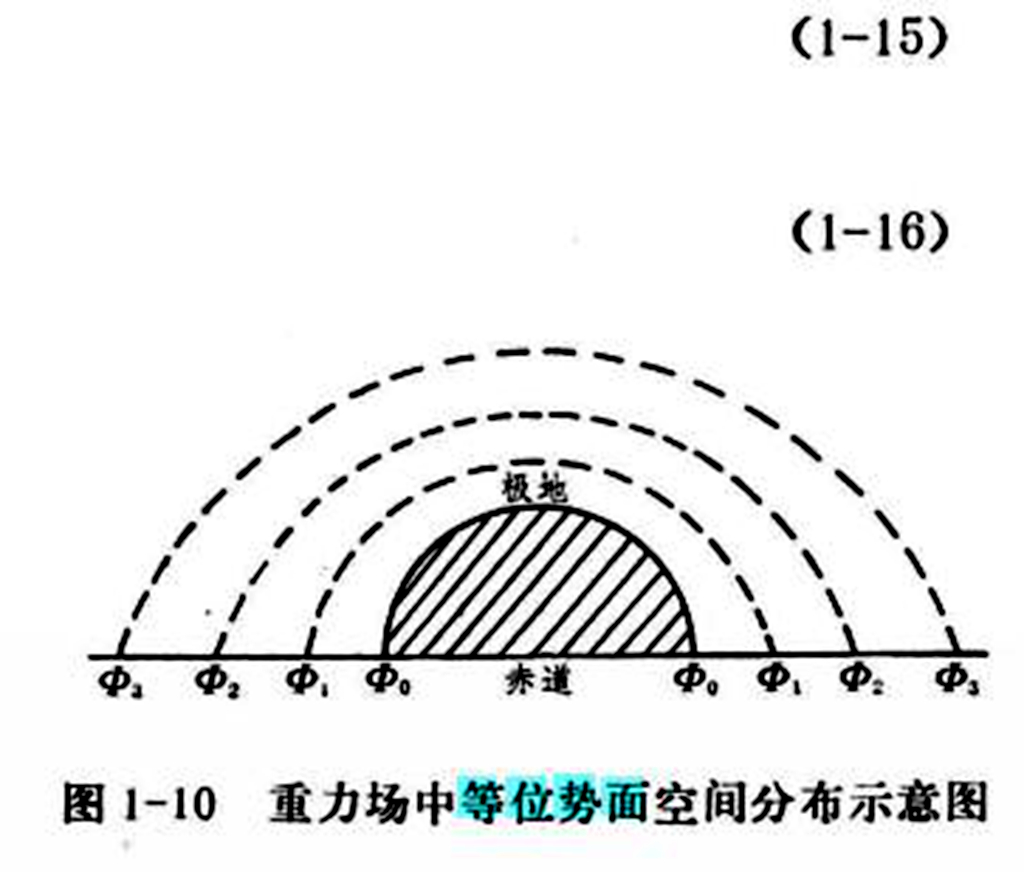
②兩等位勢面之間的幾何距離,赤道大於極地,高空大於低空。
除海平面外,等位勢面(水平面)是一個由赤道向兩極傾斜的斜面。由於赤道及高空的重力值小於兩極及低空,所以,兩等位勢面之間的距離並不相等,而是赤道大於兩極,高空大於低空。由於用等幾何高度確定的平面與等位勢面是相交的,所以,在這個平面上重力的切向分力對運動氣塊是做功的,只有等位勢面與重力垂直,沒有重力的分量,等位勢面才是真正的水平面,而等幾何高度面不是水平面。這就是我們要選用位勢單位作為決定空間位置坐標的原因。
運用及意義
重力場是地球空間最基本的物理場之一,確定地球形狀及其外部重力場是物理大地測量學研究的根本任務。隨著地球重力場模型、地面重力數據、GPS水準數據、數字地面模型(DTM)、衛星測高數據和衛星重力(SST、SGG)數據及其他地球重力場相關信息的豐富,為確定厘米級大地水準面提供了必要條件。物理大地測量隨著觀測手段的進步,人們獲得了各種不同類型的邊值,如陸地上的GPS水準、海洋上的衛星測高以及衛星重力梯度等,同時在邊值問題的理論上也由Stokes邊值、Molodensky邊值發展到如今的重力—測高邊值、重力梯度邊值等超定邊值問題。
研究學者基於厘米級似大地水準面的精度要求,對似大地水準面精化中的數據融合、精度評定等問題進行較為系統的分析,在此基礎上提出了套用GPS水準高程異常的新方法,並解決似大地水準面精化中的瓶頸問題。研究學者利用重力位模型、地面重力觀測數據、GPS水準和數字地面模型(DTM)進行似大地水準面精化。簡要闡述了最小二乘配置技術在局部重力場逼近中的套用,就最小二乘配置中的核心內容——經驗協方差函式的表達方法提出了新的估計技術;關於GPS水準在精化似大地水準面中的套用,就如何有效、合理地套用GPS水準高程異常,提出了解GPS水準超定邊值問題的算法。 有不少研究學者簡單介紹了似大地水準精化的研究進展和研究背景,並對厘米級似大地水準面精化面臨的實際問題進行簡要分析;最後介紹了大地水準面的結構和力求解決的問題。 研究就當前似大地水準面精化的基本理論做簡要敘述,如Stokes邊值問題、Molodensky邊值問題、移去—恢復法和球冠方法。