第一愛爾蘭公式（first Erlang formula）指A K．愛爾蘭給出的用於計算無限負載源全利用度損失系統呼損的公式，也稱愛爾蘭呼損公式。實際套用中要求負載源數遠大於線束容量。
基本介紹
- 中文名：第一愛爾蘭公式
- 外文名：first Erlang formula
相關概念,公式內容,套用,
相關概念
1）線束
線束為一定負載源組提供服務設備的總體，如中繼線路、交換裝置、控制系統等。話務理論的基本研究內容是研究話務量、呼損和線束容量三者之間的關係。因此，線束是話務理論中一個重要的基本概念。
負載源是線束的服務對象，通常是指用戶設備；廣義地說，上一級設備就是下一級設備的負載源。在電話通信中，負載源也稱為話源，線束中所含服務設備數，稱為線束容量。下圖是線束的示意圖。該線束的容量為V，它為N個負載源提供服務。任何一個發出呼叫的負載源，可以占用線束中的一個空閒服務設備。
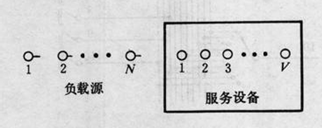圖1 線束示意圖2）全利用度線束
線束中的任意一個服務設備（中繼線或機鍵），如果都能被它所服務的負載源組中的任意一個負載源使用，則這樣的線束就稱為全利用度線束。
線束利用度指負載源組中任一個負載源所能使用的服務設備的數量。用K表示線束利用度，V表示線束容量，則有V≥K。當V=K時，線束為全利用度，利用度K的大小是受接線裝置的結構制約的。
3）呼損
當多信道共用時，由於用戶數大於信道數，可能出現許多用戶同時要求通話而信道數不能滿足要求的情況，這時只能讓一部分用戶通話，另一部分用戶不能通話，直到有空閒信道時再讓需要的用戶通話。因此一部分用戶雖然發出了呼叫，但因無信道而未能完成通話，這就稱作呼叫失敗，即發生了“呼損”。
從一個信道看，即使它在1個小時之內不間斷地進行通信，那么它所能完成的話務量也就1愛爾蘭。由於用戶發起呼叫是隨機的，不可能不間斷地持續利用信道，所以一個信道實際所能完成的話務量必定小於1愛爾蘭。這意味著，信道的利用率不可能達到百分之百。在信道共用的情況下，通信網很難保證每個用戶的所有呼叫都能成功，會有少量的呼叫失敗，稱為“呼損”。
公式內容
公式假設呼叫流為泊松分布，服務時長服從負指數分布，負載源數為無窮大，線束的容量有限。依此按時間計算的呼損率或接呼叫計算的呼損率以及接負載計算的呼損率是一樣的，並等於V條線全部被占用的機率，則第一愛爾蘭公式計算的呼損
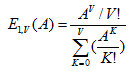
式中A為流入話務量強度，V為線束容量。此式也稱為愛爾蘭公式B。由公式還可得到它的遞推形式
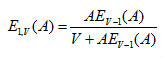
其中，泊松分布是一種統計與機率學裡常見到的離散機率分布，若隨機變數X取非負整數值k的機率為,
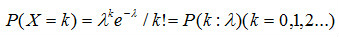
式中λ(>0)是一個參數，則X的分布稱為泊松分布,記作P(λ)。
套用
該公式適合於用電子計算機計算。目前話務工程計算中廣泛使用的愛爾蘭呼損表就是用這種公式在電子計算機上獲得的。利用這種計算表格，可以在E、A、V三者中已知其中兩個量時便可查出第三個量。
