基本介紹
- 中文名:符號方法
- 外文名:symbolic method
- 學科:計算機科學
- 定義:通過估計符號的機率值來壓縮文本
- 特點:同一時間只對一個符號編碼
- 領域:文本壓縮
定義
哈夫曼編碼
算術編碼
- 60%的機會出現符號 中性
- 20%的機會出現符號 陽性
- 10%的機會出現符號 陰性
文本壓縮
有關術語
摩爾斯電碼
機率
- 60%的機會出現符號 中性
- 20%的機會出現符號 陽性
- 10%的機會出現符號 陰性
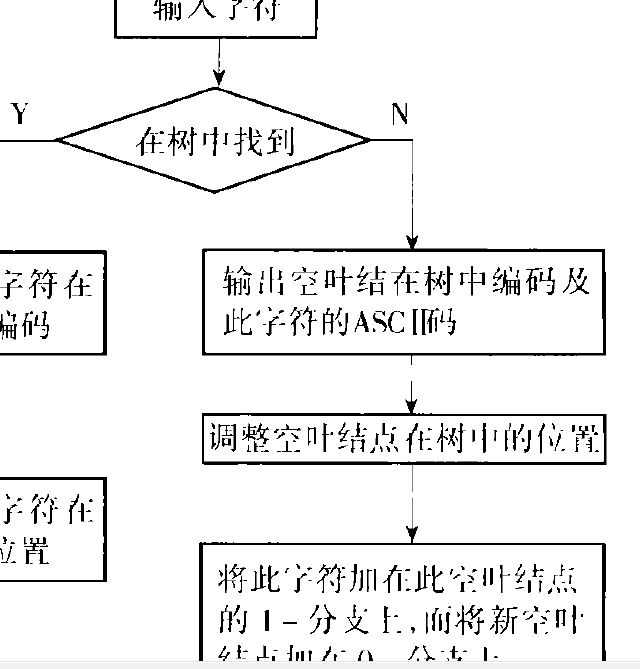
符號方法是通過估計符號(常常是字元)的機率值來壓縮文本,它在同一時間只對一個符號編碼,如摩斯碼,對最可能出現的符號使用較短的碼字。符號方法屬於外部壓縮方法,即對存儲在外部存儲器的文本數據進行壓縮,來降低數據存儲成本。定義...
西洋棋符號 ♚ ♛ ♝ ♞ ♜ ♟ ♔ ♕ ♗ ♘ ♖ ♟ 貨幣符號 ¥:人民幣符號;฿:泰銖標誌(在泰國使用)¢:分標誌(美元、歐元和其他貨幣細分);₡:科朗標誌(在哥斯大黎加和薩爾瓦多使用...
符號法是採用各種不同形狀、顏色和大小的圖形,表示各自獨立的、並以其整體概念顯示的各個物體的數量和質量特徵的方法,圖上符號的位置應與物體的實地分布位置相適應。符號法是使用很廣的表示法,常用於反映按地圖比例尺僅能以點狀表示的...
常用符號 【 】 方括弧。表示語音成分、音素或音位變體,如【∫i:p】。- 連字號。跟其他符號一起表示某個語音成分在詞中的位置,如m-表示 m出現在man中的詞首位置,-a-表示a在中間位置,-n表示n在詞末位置。: 冒號。表示對立...
加號是在計算加法時使用的計算符號。歷史 古希臘人使用加減號的方法 古希臘的丟番圖以兩數並列表示相加,偶然亦以一斜線“∕”及曲線“”分別作加號和減號使用。古印度人 一般不用加號,只有在 公元三世紀的巴赫沙里(Bakhshali)殘簡...
正確的做法是在中文輸入法下,用“shift”加上“6”組合鍵來輸入省略號,這個方法會一次打出6個小圓點。正確的字型會將這個符號造成和中文字一樣寬並上下合體(繁簡體相同)。注意事項 1、中文的省略號的形式是“……”,有6個小...
4、快捷鍵:CTRL+SHIFT+Z,特殊符號→ 輸入方法 Alt+41466(小鍵盤)含義 映射 →表示蘊涵關係,結果。例:“如果明天下雪,那么我去滑雪”。設P:明天下雪,Q:我去滑雪 得出 P→Q(指P與Q的映射關係)。轉化關係 在化學方程式中,...
輸入方法 Alt 加小數字鍵盤(Alt+42677)第一種,標準寫法,希臘字母PHi(形狀Φ,讀音fài):1、先按住Alt鍵,再在小鍵盤上輸入42677,鬆開ALT鍵就能看到了“Φ”這個符號了, (Word中和Excel電子表格中按數字 934 )。2、在Word和...
數學除了記數以外,還需要一套數學符號來表示數和數、數和形的相互關係。 數學符號的發明和使用比數字晚,但是數量多得多。常用的有200多個,國中數學書里就不下20多種。數學符號的出現 在木頭、骨頭或石頭上的計數符號從史前時代就...
變音符號 變音記號包括升號、降號、重升號、重降號和還原號,有調號和臨時記號兩種使用方法。反覆記號 從頭反覆記號:D.C. 從頭反覆。當出現Fine記號時則反覆至Fine記號結束。如圖4所示。從記號處反覆記號:D.S. 從此記號反覆到如圖...
什麼符號代表什麼意思,你可以自己掌握,但最好形成一套比較穩定的符號系統。這種方法比較適合於自學筆記和預習筆記。在操作時你應注意以下一些準則:使用原則 讀完後再做記號在你還沒有把整個段落或有標題的部分讀完並停下來思考之前,不...
這種意義論觀點在於美學和藝術研究領域中具有根本性的指導意義,引發出文藝研究中側重符號研究的一派新方法。它強調:藝術不再是客觀世界的再現,摹寫,而是一種符號體系,它蘊含著人類世界的意義,人們對它的讀解即是對世界意義的闡釋。意...
線狀符號法僅表示實地上星線狀分布的現象,不表示現象的移動和方向;能表示質量特徵,不能反映數量特徵。 中文名稱 線狀符號法 英文名稱 line symbol method 定義 以線形符號表示呈固定線狀分布的製圖對象質量與數量特徵的表示方法。 套用...
不等號(Sign of inequality)是用以表示兩個量數之間不等關係的符號。現在常用不等號包括五種:“≠”(不等號)、“> ”(大於號)、“一般地,用純粹的大於號“>”、小於號“相關背景 1629年,在法國數學家日納爾的代數教程里...
②寬窄碼。它是利用條碼寬、窄的不同所組合成的編碼。通常是寬的條形符號代表“1”,窄的條形符號代表“0”,寬與窄的比例為2:1。③有無碼。其中每一個單位距離內,有條形符號的為“1”,無條形符號的為“0”。這種編碼方式,...
特殊標點是指不常用的標點符號,代表特殊意義,也可以是有趣的標點符號。標點符號例釋 5)感動的 =@~@= 一個看到美眉就緊張+臉紅的大學生.@(一-一) 秘密---噓```(ˇ^ˇ〉 不以為然 (^人^) 拜託啦^^~(^_^)/~~ 掰掰~...
冒號是行文中常用標點符號之一,①英文半角作“:”;②英文全形作“:”;③中文全形作“:”;④中文半角作“:”。在數學語言中:①表示兩者的比值關係,如1:2,x:y,f(x):g(y);②表示兩並量的雙點積,如ab:cd=(a·c...
百分號,符號為%。指表示整數的分母是100的符號。它代表的含義:把某個整體平均分為100份,其中一部分占有的份數,即一個分數分母是100時的表示方法,也可以寫成x/100。符號介紹 百分號:表示分數的分母是100的符號(%),如32%表示...
Word文檔中的輸入方法 在Microsoft Word2010軟體插入箭頭符號的方法:第1步,打開Word2010文檔視窗,單擊需要添加箭頭符號的公式使其處於編輯狀態,並將插入條游標定位到目標位置。第2步,在“公式工具/設計”功能區的“符號”分組中單擊“...
相似符號 7. 微軟新注音及新倉頡輸入法(需按以下說明切換“中文/英數模式”或“半角/全形模式”):* 方法一:在中文模式下,按前導字元鍵(通常是鍵盤左上方的“`”)接ub7 * 方法二:在中文模式下,按Ctrl+Alt+","切換到...
打開Word文檔,打開選單欄的“插入”中“符號”,在彈出的“符號”視窗中的“字型”的下拉列表中選擇“Wingdings”,然後將滑鼠拖到最下面,你就可以看見 “√ 鉤”和 “×叉”了,選中後單擊插入即可。第二種方法:利用Word中的“...
分號(;)是一種在層次上介於逗號和句號之間的標點符號,主要用以分隔存在一定關係(並列、轉折、承接和因果等,以並列關係居多)的兩句分句——分句可以屬於單重複句,也可以是多重複句的第一層分句,或者是大句中的並列部分。單重...
