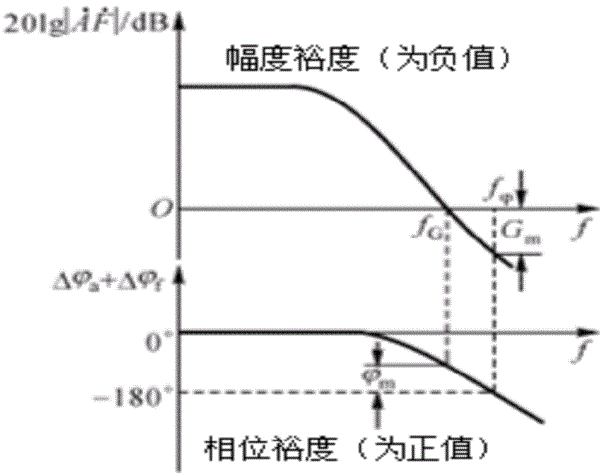
穩定裕度根據環(穩定)幅相特性曲線點的相對距離,可以判別系統的相對穩定裕度,稱之為穩定裕度。穩定裕度套用時考慮幅穩定裕度和相角穩定裕度。
基本介紹
- 中文名:穩定裕度
- 外文名:Stability margin
- 屬性:控制理論術語
- 相關:相角、裕度
- 分類:相對距離
簡介,相位裕度,相關研究,
簡介
相位裕度
相位裕度(phase margin,PM),亦稱相位餘裕,在電路設計中是非常重要的一個指標,主要用來衡量負反饋系統的穩定性,並能用來預測閉環系統階躍回響的過沖。一個性能良好的控制系統,其相位裕度應具有45°左右的數值。
相位裕度可以看作是系統進入不穩定狀態之前可以增加的相位變化,相位裕度越大,系統越穩定,但同時時間回響速度減慢了,因此必須要有一個比較合適的相位裕度。
增益裕度是以相位為裕度是-180度時的增益為準進行計算。傳統的增益裕度與相位裕度是經典頻域控制理論中的重要概念,能夠直觀在奈奎斯特圖和波德圖上表示出來,是衡量閉環控制系統魯棒性的重要性能指標。他們分別表示控制系統保持穩定條件下所能承受的最大增益擾動和最大相位擾動,以克服控制迴路中存在的干擾和對象不確定性。由於他們能夠直觀、有效的衡量控制系統的穩定性和魯棒性,基於增益、相位裕度的控制系統設計方法也受到廣泛關注。
通常開環相位延遲(相對於輸入)隨頻率變化,逐步增加到超過180°,此頻率下輸出信號(相對於輸入)反相。PM為正值,但會隨著頻率下降,在截止頻率(PM = 0)反相,於是在高頻率PM為負值(PM < 0)。在存在負反饋時,環路增益超過1情況下PM頻率為零或負值可以保證系統不穩定。因此PM為正是能保證該電路正常工作(不振盪)的“安全裕度”。這不僅適用於放大器電路,同樣適用於不同負載條件(如無功負載)下的有源濾波器。在最簡單的形式中,涉及有非抗性反饋的理想負反饋電壓放大器,在放大器的開環電壓增益等於所需閉環直流電壓增益時測定相位裕度。
更一般地,PM是由放大器及其反饋網路結合在一起(通常在放大器輸入處開環)定義的,在環路增益為1的頻率測定,並在閉合迴路之前,通過嘗試輸入源的開環輸出的方式,將其從中去除。
在上述環路增益定義中,假設放大器輸入呈現零負載。要在零負載輸入下工作,為了確定該環路增益的頻率回響,反饋網路的輸出需要加一個等效負載。
假定增益對頻率的圖象以一個負斜率穿過單位增益僅一次。只有在抗性或有源反饋網路(如有源濾波器的情形)才需要這么考慮。