定義 穆斯堡爾效應(Mössbauer effect),即原子核輻射的無反衝
共振吸收 。這個效應首先是由德國物理學家(Rudolf Ludwig Mössbauer, 1929-2011)於1958年首次在實驗中實現的,因此被命名為穆斯堡爾效應。套用穆斯堡爾效應可以研究
原子核 與周圍環境的超精細相互作用,是一種非常精確的測量手段,其能量解析度可高達10
-13 ,並且抗干擾能力強、實驗設備和技術相對簡單、對樣品無破壞。由於這些特點,穆斯堡爾效應一經發現,就迅速在物理學、化學、生物學、
冶金學 、礦物學、地質學等領域得到廣泛套用。近年來穆斯堡爾效應也在一些新興學科,如
材料科學 和表面科學開拓了套用前景。
內容詮釋 一般來說,
伽瑪射線 是由
核轉變 :從一個不穩定的高能量狀態,到一個穩定的低能量狀態。能源發出的伽瑪射線對應的能量核的過渡,再減去一些能源,是失去反衝的發光原子。如果失去了“反衝能量”是比較小的能源線寬核的過渡,那么,伽瑪射線能量仍相當於能量的核過渡和伽瑪射線可由第二個原子的同一類型第一。這以後的排放量和吸收被稱為共鳴。附加反衝能量也失去了在吸收,所以為了使
共振 發生的反衝能量必須實際上是不到一半的線寬為相應的核過渡。
從能源總量中的反衝機構可以找到
動量守恆 :圖1
圖1 其中pR是的反衝勢頭的問題,和Pγ的
伽瑪射線 勢頭。替代能源的方程為:圖2
圖2 其中ER是能源損失反衝,γ是能量的伽瑪射線,M是質量的排放或吸收的身體,c是
光速 的速度。因此大規模很小,如氣體的排放和吸收機構的
原子 ,造成大量能源反衝,防止
共振 。(請注意,同樣的方程適用於反衝能量損失在
X射線 ,但
光子 能量要小得多,從而降低能量損失,這就是為什麼氣相共振可以看到X射線。)
而作為一個整體反衝但反衝能源是微不足道的,因為M在上述方程的質量整體
晶格 。然而,能源的衰變可以採取的行動(或提供)
晶格振動 。能源這些振動單位稱為聲。
發現過程 理論上,當一個
原子核 由激發態躍遷到基態,發出一個γ射線
光子 。當這個光子遇到另一個同樣的原子核時,就能夠被
共振吸收 。但是實際情況中,處於自由狀態的原子核要實現上述過程是困難的。因為原子核在放出一個光子的時候,自身也具有了一個反衝動量,這個反衝動量會使光子的能量減少。同樣原理,吸收光子的原子核光子由於反衝效應,吸收的光子能量會有所增大。這樣造成相同
原子核 的發射譜和吸收譜有一定差異,所以自由的原子核很難實現
共振吸收 。迄今為止,人們還沒有在氣體和不太粘稠的液體中觀察到穆斯堡爾效應。
穆斯堡爾 1957年底,穆斯堡爾提出實現γ射線
共振 吸收的關鍵在於消除反衝效應。如果在實驗中把發射和吸收光子的原子核置於固體
晶格 中,那么出現反衝效應的就不再是單一的原子核,而是整個晶體。由於晶體的質量遠遠大於單一的原子核的質量,反衝能量就減少到可以忽略不計的程度,這樣就可以實現穆斯堡爾效應。實驗中原子核在發射或吸收光子時無反衝的機率叫做無反衝分數f,無反衝分數與光子能量、晶格的性質以及環境的溫度有關。
穆斯堡爾使用
191 Os(鋨)晶體作
γ射線 放射源,用
191 Ir(銥)晶體作吸收體,於1958年首次在實驗上實現了
原子核 的無反衝共振吸收。為減少熱運動對結果的影響,放射源和吸收源都冷卻到88K。放射源安裝在一個轉盤上,可以相對吸收體作前後運動,用
都卜勒效應 調節γ射線的能量。
191 Os經過β-衰變成為
191 Ir的激發態,
191 Ir的激發態可以發出能量為129 keV的γ射線,被吸收體吸收。實驗發現,當轉盤不動,即相對速度為0時
共振吸收 最強,並且
吸收譜線 的寬度很窄,每秒幾厘米的速度就足以破壞共振。除了
191 Ir外,穆斯堡爾還觀察到了
187 Re、
177 Hf、
166 Er等原子核的無反衝共振吸收。由於這些工作,穆斯堡爾被授予1961年的
諾貝爾物理學獎 。
發生原因 穆斯堡爾效應的發生原因,是因為那裡是一種有限的機率發生衰變不涉及聲。因此,在一小部分的核事件(坐無分數),整個晶體作為反衝機構,這些事件基本上是坐無。在這些例子中,因為坐的能源是微不足道的,發出的
伽瑪射線 具有適當的能量和
共振 可以發生。一般(取決於半衰期衰變),伽瑪射線有非常狹隘的線寬。這意味著他們是非常敏感的小變化,能量的核過渡。事實上,γ射線可以用來作為探針觀察相互作用及其核電子和它的鄰居。這是基礎,穆斯堡爾譜,它結合了穆斯堡爾效應的都卜勒效應來監測這種相互作用。
穆斯堡爾光譜儀 零
聲光 轉換,這個過程類似於密切的穆斯堡爾效應,可以看到
晶格 方向發色團在低溫條件下。
實際套用 截至2005年上半年,人們已經在固體和粘稠液體中實現了穆斯堡爾效應,樣品的形態可以是晶體、
非晶體 、薄膜、固體表層、粉末、顆粒、冷凍溶液等等,涉及40餘種元素90餘種同位素的110餘個躍遷。然而大部分同位素只能在低溫下才能實現穆斯堡爾效應,有的需要使用
液氮 甚至
液氦 對樣品進行冷卻。在室溫下只有
57 Fe、
119 Sn、
151 Eu三種同位素能夠實現穆斯堡爾效應。其中
57 Fe的 14.4 keV 躍遷是人們最常用的、也是研究最多的譜線。
粒子躍遷 實驗條件 穆斯堡爾效應對環境的依賴性很高。細微的環境條件差異會對穆斯堡爾效應產生顯著的影響。在實驗中,為減少環境帶來的影響,需要利用都卜勒效應對
γ射線 光子 的能量進行細微的調製。具體做法是令γ射線輻射源和吸收體之間具有一定的相對速度,通過調整v的大小來略微調整γ射線的能量,使其達到
共振吸收 ,即吸收率達到最大,
透射率 達到最小。透射率與相對速度之間的變化曲線叫做
穆斯堡爾譜 。套用穆斯堡爾譜可以清楚地檢查到
原子核 能級的移動和分裂,進而得到原子核的超精細場、原子的價態和
對稱性 等方面的信息。套用穆斯堡爾譜研究原子核與核外環境的超精細相互作用的學科叫做
穆斯堡爾譜學 。請參考條目穆斯堡爾譜學。
穆斯堡爾譜的寬度非常窄,因此具有極高的能量
分辨本領 。例如
57 Fe的 14.4 keV 躍遷,穆斯堡爾譜寬度與γ射線的能量之比ΔE/E~10
-13 ,
67 Zn的 93.3 keV 躍遷ΔE/E~10
-15 ,
107 Ag的93 keV 躍遷ΔE/E~10
-22 。因此穆斯堡爾效應一經發現就在各種精密頻差測量中得到廣泛套用。
實驗套用 測量
引力紅移 —— 引力引起的紅移量一般小於10
-10 數量級,歷史上套用穆斯堡爾效應首先對其進行了精密測量。
相對論 預言,由於地球上不同高度
引力勢能 不同,會引起
光子 離開
地球時 在不同高度的頻率不同,相差20米帶來的頻率測量變化為2×10
-15 。1960年,龐德和里布卡利用穆斯堡爾效應測量到了這個微小的變化 。
引力紅移 在中國,世界公認的最傑出的女性物理學家,被譽為“核子物理女皇”和中國的居里夫人的
吳健雄 ,在1959年穆斯堡爾效應發現之後,吳健雄對它進行了深入的研究,將穆斯堡爾
光譜法 用於生物學中大分子的結構研究。為了證實
輕子數 在
弱作用 中守恆律的有效性,吳健雄等在深達2000餘英尺的純鹽礦中安置了測量
雙β衰變 儀器,證明了輕子數守恆到10
-3 以上。在類似問題上,也得到了解決和證明或一定程度上的澄清。
驗證麥可遜-莫雷實驗
1970年,伊薩克(G.R.Isaak)利用穆斯堡爾效應測量了地球相對於
以太 的速度 。
實驗原理是基於經典力學都卜勒頻移結果。假設一頻率為f的光波包在以太靜止參考系K中傳播,參考系K’相對參考系以速度v運動。則在K’參考系中波包產生頻移。
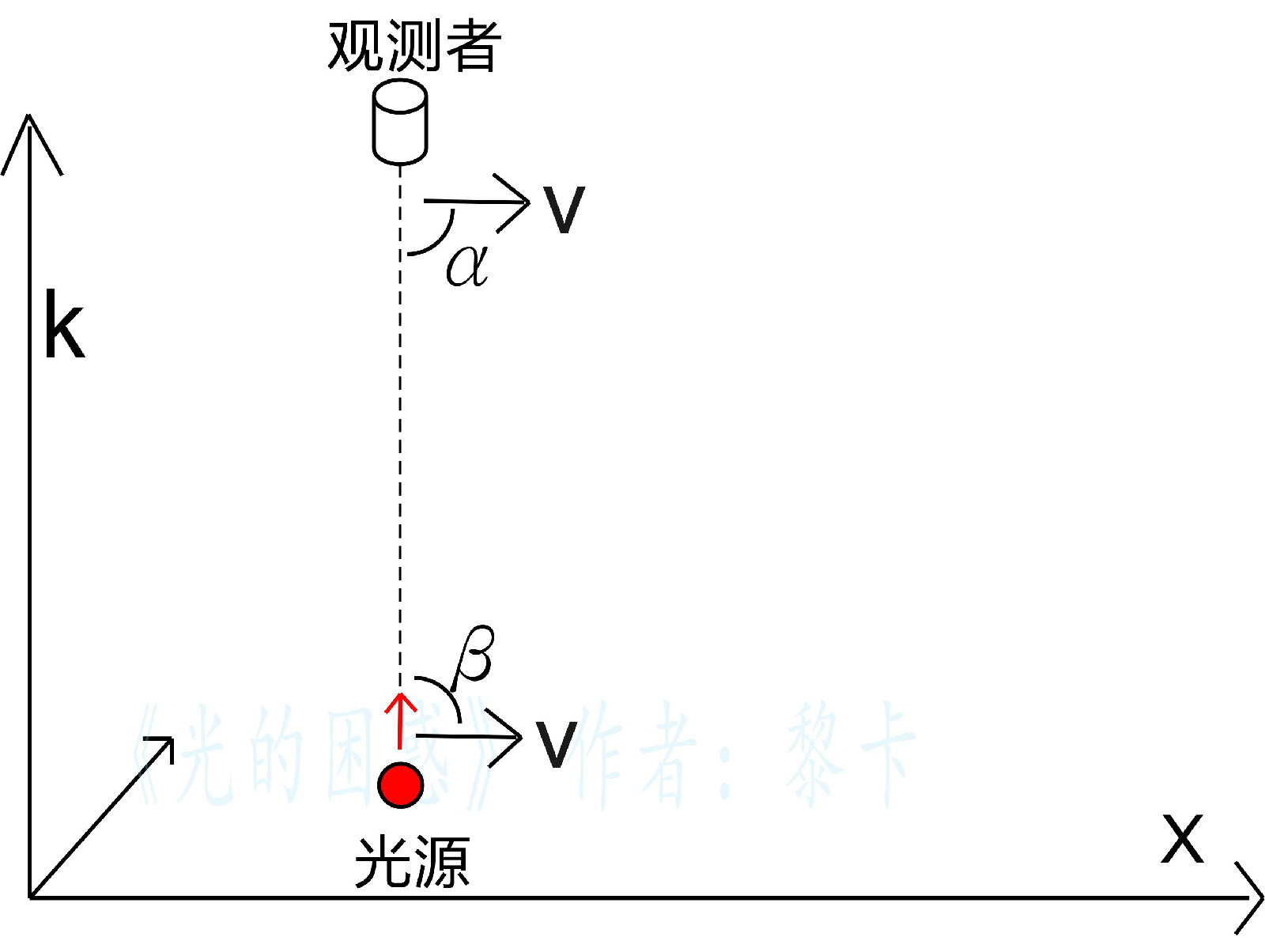
在運動參考系K'中,波包垂直X軸向上運動。去掉K'參考系,在以太靜止參考系K中波包的運動和觀測者的運動如圖所示。波包和觀測者在X軸方向有同向運動,則觀測者觀測到波包頻率產生紅移,去掉觀測者,就是說在K'參考系中波包頻率紅移。所以經典力學都卜勒頻移認為從移動光源運動方向垂直方向觀測移動光源產生紅移。
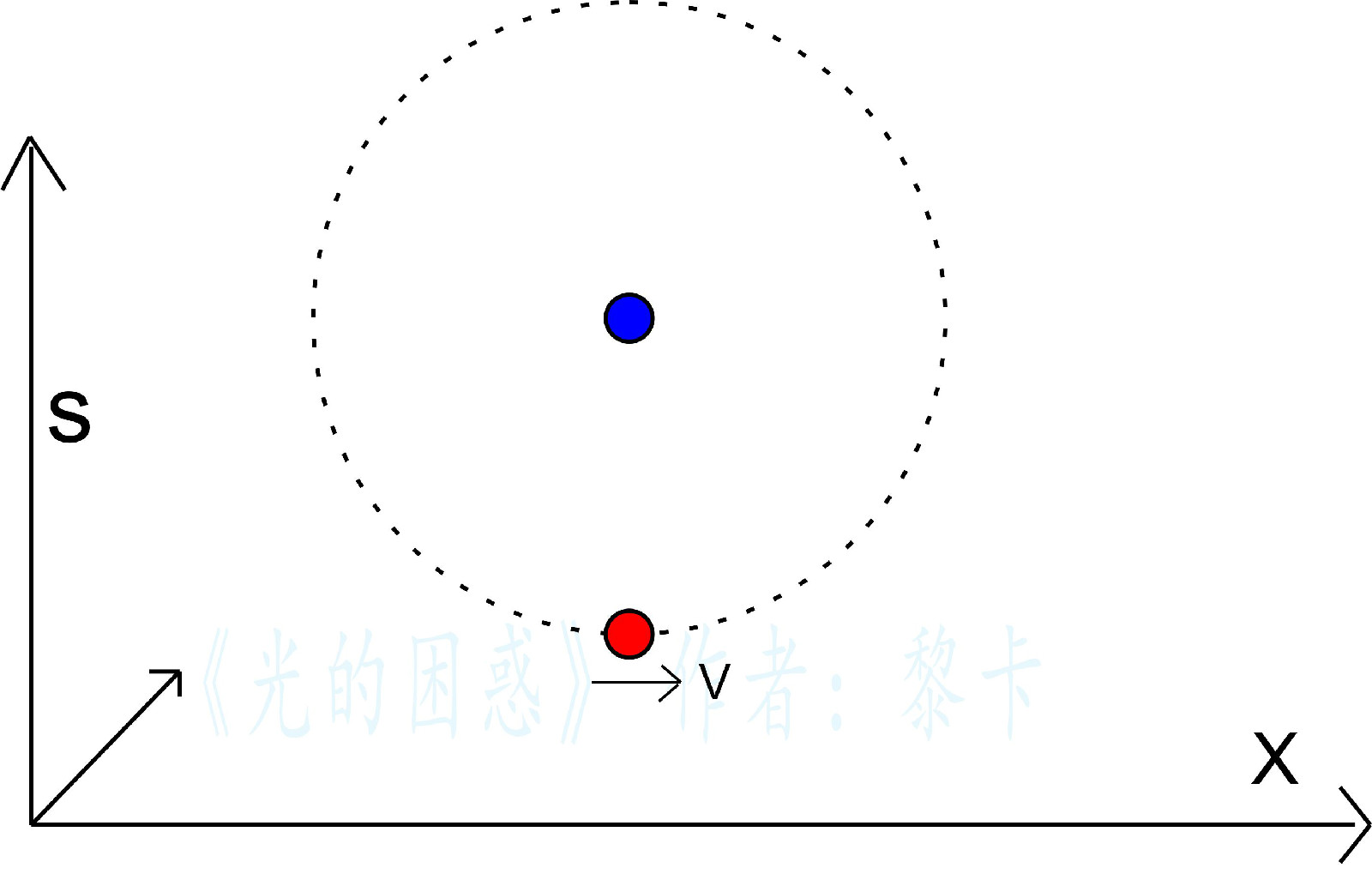
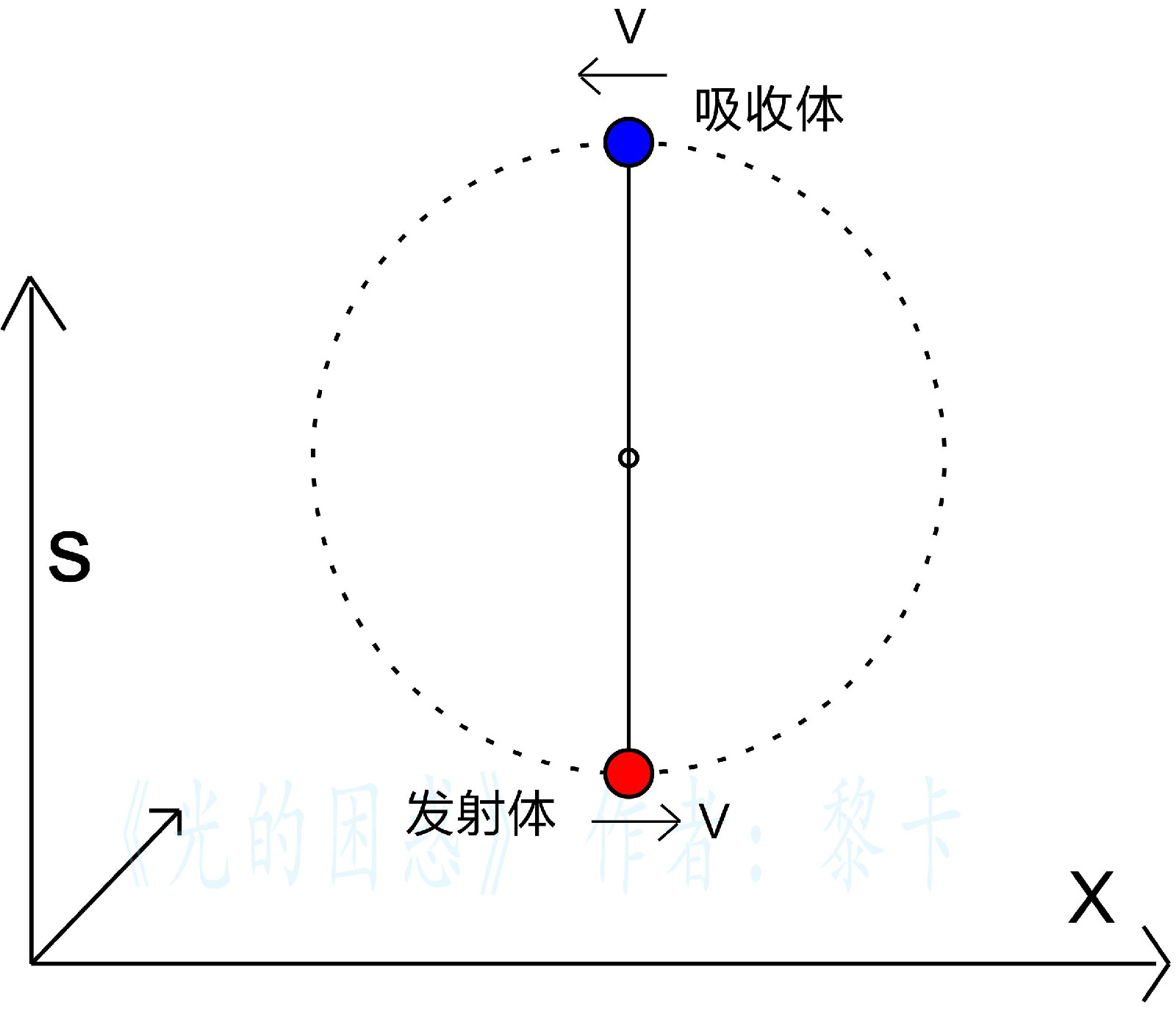
在S參考系中紅球圍繞藍球做圓周運動。如果S參考系在以太中靜止,以運動的紅球為參考系,則運動方向法線上的藍球觀測到紅球發出的光波產生紅移。如果S參考系在以太中運動,速度為U,則紅球在以太中運動速度從U+V到U-V規律變化。以紅球為參考系,法線上的藍球觀測到紅球發出的光波產生紅移也隨之規律變化。
穆斯堡爾效應以太漂移實驗為一發射體和一吸收體放在一根長為2R的木棍兩端,木棍圍繞其中心運動。則吸收體觀測到紅球的頻移變化翻倍。實驗測得以太速度的上限為5×10
-5 km/s,基本證實了不存在地球相對於
以太 的運動。
以太飄移實驗原理質疑
上述分析中, 使用了脫離光源的波包,假定脫離光源的波包頻率恆定(頻率恆定的是光源,而不是波包),並用參考系替代觀測者,所以對問題的分析比較片面。要全面分析都卜勒效應不能離開波源與觀測者。
也有人對運動光源垂直方向觀測光源產生紅移的理解是:當波包離開光源後在靜止以太參考系中運動,那么在運動的K參考系中波包的運動方向與光源的運動方向夾角β大於90度。而觀測者運動與波包運動方向正好垂直,即α等於90度。這個理解也有誤區,因為波源運動方向與波包運動方向的夾角值β大於90度是以靜止的以太參考係為準,而觀測者運動方向與波包運動方向的夾角值α等於90度是以運動參考係為準。
對該問題的合理分析必須要在同一個參考系中。在運動參考系保持靜止的觀測者與光源,在絕對靜止的參考系中他們的運動速度與方向相同。則夾角α +β =180度。根據經典力學都卜勒頻移公式
=
計算可得出觀測者與光源不產生頻移。
從移動光源運動方向垂直方向觀測移動光源不一定產生紅移,所以穆斯堡爾效應以太飄移實驗從原理上不合理。

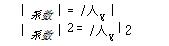 圖1
圖1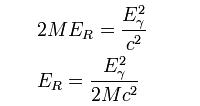 圖2
圖2 穆斯堡爾光譜儀
穆斯堡爾光譜儀 粒子躍遷
粒子躍遷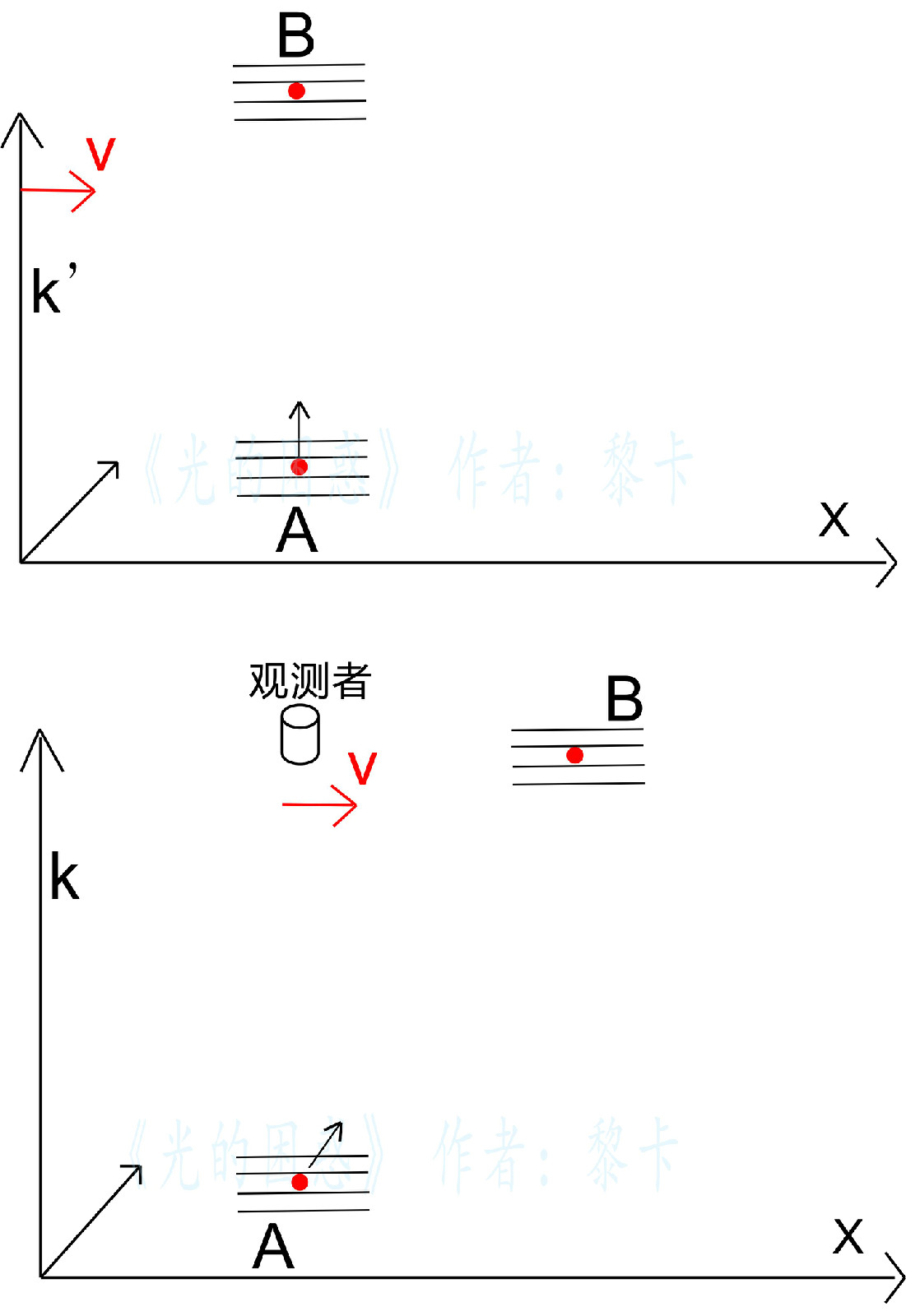


 穆斯堡爾
穆斯堡爾 引力紅移
引力紅移