基本介紹
- 中文名:程式設計語言語義
- 外文名:programming language semantics
- 學科:計算機
- 定義:指明給出程式設計語言的程式含義
- 有關術語:語義
- 領域:程式語言
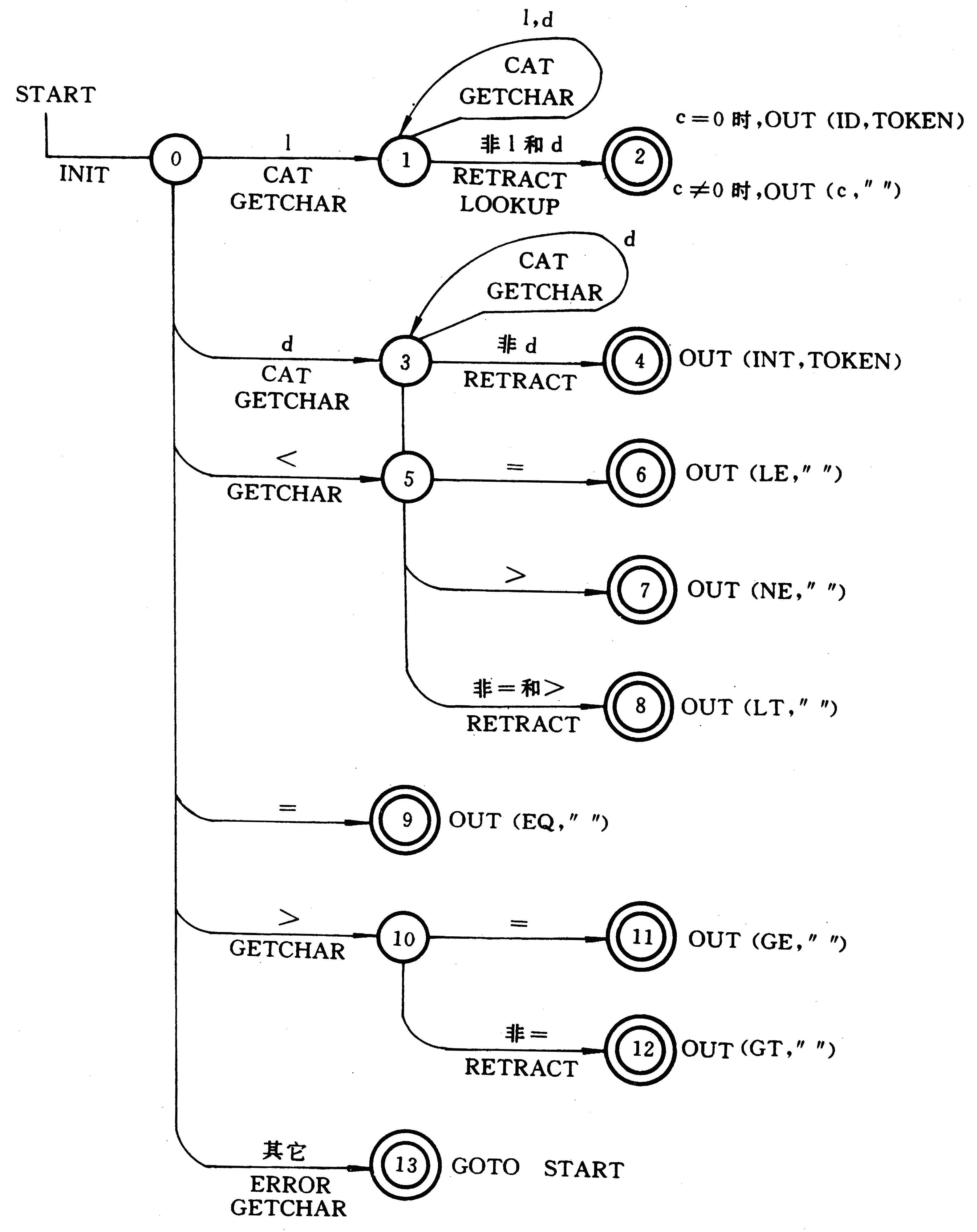
語法和語義是定義一個程式設計語言所涉及的兩個重要側面:語法涉及程式文法結構,研究程式設計語言所允許的成分結構形式;而語義則涉及文法上正確的程式的含義,研究語言...
《程式設計語言的形式語義》是2004年機械工業出版社出版的圖書,作者是GlynN Winskel。...
程式設計語言是用於書寫電腦程式的語言。語言的基礎是一組記號和一組規則。根據規則由記號構成的記號串的總體就是語言。在程式設計語言中,這些記號串就是程式。...
《程式設計語言理論》是2004年高等教育出版社出版的圖書,作者是陳意雲。該書主要講述了分析程式設計語言語法、操作和語義性質的一個基於λ演算系統框架。...
形式語義學(formal semantics),是程式設計理論的組成部分,以數學為工具,利用符號和公式,精確地定義和解釋計算機程式設計語言的語義,使語義形式化的學科。形式語義學是...
面向對象程式設計(Object Oriented Programming,OOP)的實質是選用一種面向對象程式設計語言(OOPL),採用對象、類及其相關概念所進行的程式設計。...
《程式設計語言原理》是2011年北京航空航天大學出版社出版的圖書,作者是麥中凡。...... 第15章 描述性程式設計語言第16章 指稱語義的原理與套用第17章 代數語義學...
《程式設計語言——實踐之路》是由電子工業出版社出版,作者Michael L.Scott,譯者裘宗燕。...
《程式設計語言與編譯:語言的設計與實現(第4版)》是2015年3月電子工業出版社出版的圖書,作者是王曉斌。...
這是一本很有特色的教材,其核心是討論程式設計語言的工作原理和技術。本書融合了傳統的程式設計語言教科書和編譯教科書的有關知識,並增加了一些有關彙編層體系結構...
《程式設計語言:編譯原理》是2006年3月1日國防工業出版社出版的圖書。...... 《程式設計語言:編譯原理》(第3版)是在...語義分析與中間代碼產生、符號表與運行時...
《程式設計語言理論基礎》是2006年電子工業出版社出版的圖書,作者是(美)米切爾。本書提出了一個框架,用於分析程式設計語言的語法、操作和語義性質,該框架基於稱為...
程式設計是給出解決特定問題程式的過程,是軟體構造活動中的重要組成部分。程式設計往往以某種程式設計語言為工具,給出這種語言下的程式。程式設計過程應當包括分析、...
《程式設計語言概念》為程式設計師寫出一個好的程式提供了所需的抽象機制、組織原則以及控制結構。本書所介紹的是在程式設計語言中出現的概念,即在程式設計語言的實現...
《程式設計語言概念(第9版)》是2011年1月清華大學出版社出版的圖書,作者是Robert W.Sebesta、譯者徐明星。...
形式語義學的一個分支。人們用程式設計語言編製程序,命令計算機系統去加工數據。不同的計算機系統有不同的結構,因此對同一個命令的執行過程可以不同,但最終效果應該...
在高級程式設計語言翻譯中,語義分析階段的工作不與目標機器的體系結構密切相關,而目標代碼生成階段的工作與目標機器的體系結構密切相關。...
《D程式設計語言》是2013年人民郵電出版社出版的圖書,作者是美AndreiAlexandrescu。...
人工智慧(AI)語言是一類適應於人工智慧和知識工程領域的、具有符號處理和邏輯推理能力的計算機程式設計語言。能夠用它來編寫程式求解非數值計算、知識處理、推理、規劃...
可擴充程式設計語言是一種具有擴充機制的程式設計語言,如ALGOL、Forth語言。一個程式設計語言稱為可擴充的是指用戶能根據自己的需要,利用該語言提供的擴充手段,往該...
《類型和程式設計語言》是2005年電子工業出版社出版的圖書,作者是皮爾斯。...... 《類型和程式設計語言》是2005年電子工業...設計本身,幫助運行系統檢查程式中的語義...
操作語義學,是形式語義學的一個分支。程式設計語言的實施是在具體的計算機系統中按照語言的語義編制語言的翻譯程式,將語言中各個成分翻譯成計算機系統中相應的一組...
本書介紹了指稱語義學、代數語義學、操作語義學與公理語義學的基本內容及其套用,並介紹了並發程式設計語言各流派的語義模型和新一代計算機計算模型的理論問題。...
程式設計語言有幾十年的發展、套用的歷史,了解其發展和分類有助於在軟體開發中選擇合適的程式設計語言。隨著程式設計語言的發展,出現了很多軟體開發工具,其充分展示...
函式式程式設計是一種設計、編制和調試函式式程式的技術,是由一些原始函式、定義函式和函式型組成的函式表達式。函式語言以λ-演算為其語義基礎, 它的基本機制是...
由於函式式程式設計語言的簡明性和獨特的表達能力,可用它來研究傳統程式設計語言的語義。一種方法是用於確定一個解釋程式的定義,作為被研究的語言的語義;另一種方法...
《程式設計語言與編譯:語言的設計和實現》為“普通高等教育‘十一五’國家級規劃教材”,是一本計算機專業的寬口徑教材,新版覆蓋CC2001和CCC2002教程中,除自動機外...
GML(GameMaker Language)是一種解釋性程式設計語言。它被設計成用於一個稱為“GameMaker”的遊戲引擎的腳本語言,它最初由Mark Overmars創建,用於補充Game Maker中...
