稀薄點

稀薄點是描述密度的另一個概念。設E是R中的勒貝格可測集，當E在點x0處的密度等於0時，則稱x0為E的稀薄點。

基本介紹

• 中文名：稀薄點
• 外文名：point of rarity
• 適用範圍：數理科學

簡介

稀薄點是描述密度的另一個概念。

設E是R中的勒貝格可測集，當E在點x₀處的密度等於0時，即

則稱x₀為E的稀薄點。

密度

設E是R中勒貝格可測集，對於任意一點x₀，記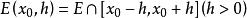

，如果極限存在，則稱它為E在點x₀處的密度。

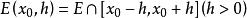
勒貝格可測集

勒貝格可測集是實變函式論的重要概念之一，指勒貝格意義下可求“長度”、“面積”或“體積”的一類集合。

若m*為Rⁿ上的(L)外測度，E⊂Rⁿ且滿足卡拉西奧多條件，即對任意點集T⊂Rⁿ，有

則稱集E為勒貝格可測集，簡稱(L)可測集。