稀疏自編碼器是一種無監督機器學習算法,通過計算自編碼的輸出與原輸入的誤差,不斷調節自編碼器的參數,最終訓練出模型。自編碼器可以用於壓縮輸入信息,提取有用的輸入特徵。
基本介紹
- 中文名:稀疏自編碼器
- 外文名:Sparse Autoencoder
- 領域:深度學習
提出思路
算法原理
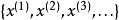
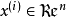
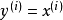
 圖一
圖一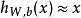
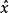


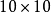
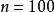

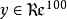
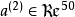

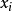
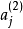


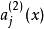


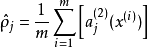
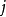
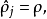
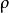
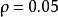
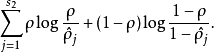
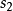
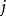
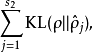
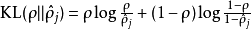
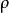
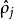
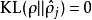
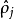
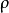
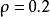
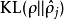

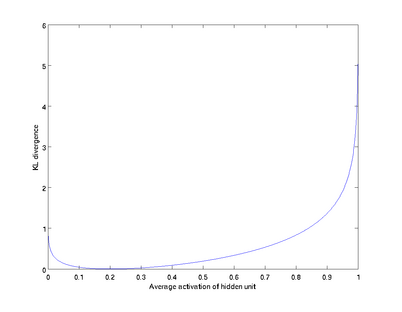 圖二
圖二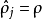
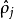
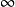
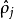

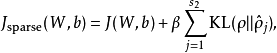
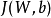
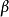
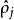
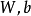

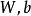
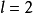
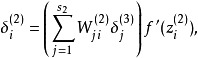
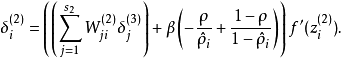
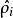
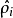
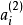
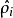
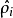
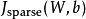
與自動編碼器的區別
 圖三
圖三為什麼要用稀疏自編碼器
如果給定一個神經網路,我們假設其輸出與輸入是相同的,然後訓練調整其參數,得到每一層中的權重。自然地,我們就得到了輸入的幾種不同表示(每一層代表一種表示),這些表示就是特徵。自動編碼器就是一種儘可能復現輸入信號的神經網路。為了實現這種復現,自動編碼器就必須捕捉可以代表輸入數據的最重要的因素,就像PCA那樣,找到可以代表原信息的主要成分。
當然,我們還可以繼續加上一些約束條件得到新的Deep Learning方法,如:如果在AutoEncoder的基礎上加上L1的Regularity限制(L1主要是約束隱含層中的節點中大部分都要為0,只有少數不為0,這就是Sparse名字的來源),我們就可以得到Sparse AutoEncoder法。
之所以要將隱含層稀疏化,是由於,如果隱藏神經元的數量較大(可能比輸入像素的個數還要多),不稀疏化我們無法得到輸入的壓縮表示。具體來說,如果我們給隱藏神經元加入稀疏性限制,那么自編碼神經網路即使在隱藏神經元數量較多的情況下仍然可以發現輸入數據中一些有趣的結構。
稀疏自編碼器的解釋
通過tensorflow實現的稀疏自編碼器
初始化參數
input_nodes = 8*8 //輸入節點數hidden_size = 100//隱藏節點數output_nodes = 8*8//輸出節點數
初始化訓練集數據
def sampleImage(): mat = scipy.io.loadmat('F:/ml/code/IMAGES.mat') pic = mat['IMAGES'] shape = pic.shape patchsize = 8 numpatches = 1000 patches = [] i = np.random.randint(0, shape[0]-patchsize,numpatches) j = np.random.randint(0, shape[1]-patchsize, numpatches) k = np.random.randint(0, shape[2], numpatches) for l in range(numpatches): temp = pic[i[l]:(i[l]+patchsize), j[l]:(j[l]+patchsize), k[l]] temp = temp.reshape(patchsize*patchsize) patches.append(temp) return patches通過xvaier初始化第一層的權重值
def xvaier_init(input_size, output_size): low = -np.sqrt(6.0/(input_nodes+output_nodes)) high = -low return tf.random_uniform((input_size, output_size), low, high, dtype = tf.float32)
計算代價函式
def computecost(w,b,x,w1,b1): p = 0.1 beta = 3 lamda = 0.00001 hidden_output = tf.sigmoid(tf.matmul(x,w) + b) pj = tf.reduce_mean(hidden_output, 0) sparse_cost = tf.reduce_sum(p*tf.log(p/pj)+(1-p)*tf.log((1-p)/(1-pj))) output = tf.sigmoid(tf.matmul(hidden_output,w1)+b1) regular = lamda*(tf.reduce_sum(w*w)+tf.reduce_sum(w1*w1))/2 cross_entropy = tf.reduce_mean(tf.pow(output - x, 2))/2 +sparse_cost*beta + regular #+ regular+sparse_cost*beta return cross_entropy, hidden_output, output
可視化自編碼器
def show_image(w): sum = np.sqrt(np.sum(w**2, 0)) changedw = w/sum a,b = changedw.shape c = np.sqrt(a*b) d = int(np.sqrt(a)) e = int(c/d) buf = 1 newimage = -np.ones((buf+(d+buf)*e,buf+(d+buf)*e)) k = 0 for i in range(e): for j in range(e): maxvalue = np.amax(changedw[:,k]) if(maxvalue<0): maxvalue = -maxvalue newimage[(buf+i*(d+buf)):(buf+i*(d+buf)+d),(buf+j*(d+buf)):(buf+j*(d+buf)+d)] = np.reshape(changedw[:,k],(d,d))/maxvalue k+=1 plt.figure("beauty") plt.imshow(newimage) plt.axis('off') plt.show() 主函式
def main(): w = tf.Variable(xvaier_init(input_nodes, hidden_size)) b = tf.Variable(tf.truncated_normal([hidden_size],0.1)) x = tf.placeholder(tf.float32, shape = [None, input_nodes]) w1 = tf.Variable(tf.truncated_normal([hidden_size,input_nodes], -0.1, 0.1)) b1 = tf.Variable(tf.truncated_normal([output_nodes],0.1)) cost, hidden_output, output = computecost(w,b,x,w1,b1) train_step = tf.train.AdamOptimizer().minimize(cost) train_x = sampleImage() sess = tf.Session() sess.run(tf.global_variables_initializer()) for i in range(100000): _,hidden_output_, output_,cost_,w_= sess.run([train_step, hidden_output, output,cost,w], feed_dict = {x : train_x}) if i%1000 == 0: print(hidden_output_) print(output_) print(cost_) np.save("weights1.npy", w_) show_image(w_)
