收縮自編碼器

收縮自編碼器(contractive autoencoder，CAE)是一種正則自編碼器。它在編碼h=f(x)的基礎上添加了顯示的正則項，鼓勵 f 的導數儘可能小，它的懲罰項Ω(h) 是平方Frobenius範數（元素平方的和），作用於與編碼器的函式相關偏導數的Jacobian矩陣。

基本介紹

• 中文名：收縮自編碼器
• 外文名：contractive autoencoder
• 屬於：正則自編碼器
• 收縮：源於CAE彎曲空間的方式
• 性質：只在局部收縮
• 目標：學習數據的流形結構

自編碼器

自編碼器（autoencoder）是神經網路的一種，經過訓練後能嘗試將輸入複製到輸出。 自編碼器內部有一個隱藏層 ，可以產生編碼（code）表示輸入。該網路可以看作由兩部分組成：一個由函式 表示的編碼器和一個生成重構的解碼器 。

如圖1，為自編碼器一般結構。通過內部表示或編碼 將輸入 映射到輸出（稱為重構） 。 自編碼器具有兩個組件： 編碼器 （將 映射到 ）和解碼器 （將 映射到 ）。

圖 1 自編碼器一般結構

如果一個自編碼器只是簡單地學會將處處設定為 ，那么這個自編碼器就沒什麼特別的用處。相反，我們不應該將自編碼器設計成輸入到輸出完全相等。這通常需要向自編碼器強加一些約束，使它只能近似地複製，並只能複製與訓練數據相似的輸入。這些約束強制模型考慮輸入數據的哪些部分需要被優先複製，因此它往往能學習到數據的有用特性。

現代自編碼器將編碼器和解碼器的概念推而廣之，將其中的確定函式推廣為隨機映射 和 。

數十年間， 自編碼器的想法一直是神經網路歷史景象的一部分。傳統自編碼器被用於降維或特徵學習。近年來， 自編碼器與潛變數模型理論的聯繫將自編碼器帶到了生成式建模的前沿，我們將在第二十章揭示更多細節。 自編碼器可以被看作是前饋網路的一個特例，並且可以使用完全相同的技術進行訓練，通常使用小批量梯度下降法（其中梯度基於反向傳播計算）。不同於一般的前饋網路， 自編碼器也可以使用循環（recirculation）訓練，這種學習算法基於比較原始輸入的激活和重構輸入的激活。相比反向傳播算法， 再循環算法更具生物學意義，但很少用於機器學習套用。

正則自編碼器

編碼維數小於輸入維數的欠完備自編碼器可以學習數據分布最顯著的特徵。我們已經知道，如果賦予這類自編碼器過大的容量，它就不能學到任何有用的信息。

如果隱藏編碼的維數允許與輸入相等，或隱藏編碼維數大於輸入的 過完備（overcomplete）情況下，會發生類似的問題。在這些情況下，即使是線性編碼器和線性解碼器也可以學會將輸入複製到輸出，而學不到任何有關數據分布的有用信息。

理想情況下，根據要建模的數據分布的複雜性，選擇合適的編碼維數和編碼器、解碼器容量，就可以成功訓練任意架構的自編碼器。正則自編碼器提供這樣的能力。正則自編碼器使用的損失函式可以鼓勵模型學習其他特性（除了將輸入複製到輸出），而不必限制使用淺層的編碼器和解碼器以及小的編碼維數來限制模型的容量。這些特性包括稀疏表示、 表示的小導數、以及對噪聲或輸入缺失的魯棒性。即使模型容量大到足以學習一個無意義的恆等函式，非線性且過完備的正則自編碼器仍然能夠從數據中學到一些關於數據分布的有用信息。

除了這裡所描述的方法（正則化自編碼器最自然的解釋），幾乎任何帶有潛變數並配有一個推斷過程（計算給定輸入的潛在表示）的生成模型，都可以看作是自編碼器的一種特殊形式。強調與自編碼器聯繫的兩個生成式建模方法是 Helmholtz機的衍生模型，如變分自編碼器和生成隨機網路。這些變種（或衍生） 自編碼器能夠學習出高容量且過完備的模型，進而發現輸入數據中有用的結構信息，並且也無需對模型進行正則化。這些編碼顯然是有用的，因為這些模型被訓練為近似訓練數據的機率分布而不是將輸入複製到輸出。

表達式

在正則自編碼器中，其中一種是使用一個類似稀疏自編碼器中的懲罰項 ，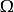

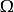
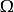
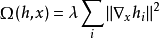
但 的形式不同，

這迫使模型學習一個在 變化小時目標也沒有太大變化的函式。因為這個懲罰只對訓練數據適用，它迫使自編碼器學習可以反映訓練數據分布信息的特徵。

這樣正則化的自編碼器稱為收縮自編碼器（contractive autoencoder，CAE）。這種方法與去噪自編碼器、流形學習和機率模型存在一定的理論聯繫。

收縮自編碼器在編碼 h = f(x) 的基礎上添加了顯式的正則項，鼓勵 的導數儘可能小：

懲罰項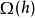 為平方 Frobenius 範數（元素平方之和），作用於與編碼器的函式相關偏導數的 Jacobian 矩陣。

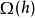
含義

去噪自編碼器和收縮自編碼器之間存在一定聯繫： 在小高斯噪聲的限制下，當重構函式將 x 映射到 時，去噪重構誤差與收縮懲罰項是等價的。換句話說， 去噪自編碼器能抵抗小且有限的輸入擾動，而收縮自編碼器使特徵提取函式能抵抗極小的輸入擾動。

分類任務中，基於 Jacobian 的收縮懲罰預訓練特徵函式 ，將收縮懲罰套用在 而不是 g(f(x)) 可以產生最好的分類精度。套用於 的收縮懲罰與得分匹配也有緊密的聯繫。

收縮（contractive）源於 CAE 彎曲空間的方式。具體來說，由於 CAE 訓練為抵抗輸入擾動，鼓勵將輸入點鄰域映射到輸出點處更小的鄰域。我們能認為這是將輸入的鄰域收縮到更小的輸出鄰域。說得更清楚一點， CAE 只在局部收縮——一個訓練樣本 的所有擾動都映射到 的附近。全局來看，兩個不同的點 x 和 x′ 會分別被映射到遠離原點的兩個點 和 。 擴展到數據流形的中間或遠處是合理的。當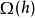 懲罰套用於 sigmoid 單元時， 收縮 Jacobian 的簡單方式是令 sigmoid 趨向飽和的 0 或 1。這鼓勵 CAE 使用 sigmoid 的極值編碼輸入點，或許可以解釋為二進制編碼。它也保證了 CAE 可以穿過大部分 sigmoid 隱藏單元能張成的超立方體，進而擴散其編碼值。

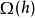
我們可以認為點 處的 Jacobian 矩陣 能將非線性編碼器近似為線性運算元。這允許我們更形式地使用 “收縮’’ 這個詞。線上性理論中，當 的範數對於所有單位 都小於等於 1 時， 被稱為收縮的。換句話說，如果 收縮了單位球，他就是收縮的。我們可以認為 CAE 為鼓勵每個局部線性運算元具有收縮性，而在每個訓練數據點處將 Frobenius 範數作為 的局部線性近似的懲罰。

正則自編碼器基於兩種相反的推動力學習流形。在 CAE 的情況下，這兩種推動力是重構誤差和收縮懲罰 Ω(h)。單獨的重構誤差鼓勵 CAE 習一個恆等函式。單獨的收縮懲罰將鼓勵 CAE 學習關於 x 是恆定的特徵。這兩推動力的的折衷產生導數 大多是微小的自編碼器。只有少數隱藏單元，對應一小部分輸入數據的方向，可能有顯著的導數。

目標

CAE 的目標是學習數據的流形結構。使 很大的方向 ，會快速改變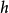 ，因此很可能是近似流形切平面的方向。訓練 CAE 會導致 J 中大部分奇異值（幅值）比 1 小，因此是收縮的。然而，有些奇異值仍然比1 大，因為重構誤差的懲罰鼓勵 CAE 對最大局部變化的方向進行編碼。對應於最大奇異值的方向被解釋為收縮自編碼器學到的切方向。理想情況下，這些切方向應對應於數據的真實變化。比如，一個套用於圖像的 CAE 應該能學到顯示圖像改變的切向量。

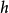
實際問題

收縮自編碼器正則化準則的一個實際問題是，儘管它在單一隱藏層的自編碼器情況下是容易計算的，但在更深的自編碼器情況下會變的難以計算。根據 Rifai et al. (2011a) 的策略，分別訓練一系列單層的自編碼器，並且每個被訓練為重構前一個自編碼器的隱藏層。這些自編碼器的組合就組成了一個深度自編碼器。因為每個層分別訓練成局部收縮，深度自編碼器自然也是收縮的。這個結果與聯合訓練深度模型完整架構（帶有關於Jacobian的懲罰項）獲得的結果是不同的，但它抓住了 許多理想的定性特徵。

另一個實際問題是，如果我們不對解碼器強加一些約束， 收縮懲罰可能導致無用的結果。例如， 編碼器將輸入乘一個小常數 ϵ， 解碼器將編碼除以一個小常數 。隨著 趨向於 0， 編碼器會使收縮懲罰項 Ω(h) 趨向於 0 而學不到任何關於分布的信息。同時， 解碼器保持重構。 Rifai et al. (2011a) 通過綁定 和 的權重來防止這種情況。 和 都是由線性仿射變換後進行逐元素非線性變換的標準神經網路層組成，因此將 的權重矩陣設成 權重矩陣的轉置是很直觀 。