稀疏傅立葉變換(Sparse Fourier Transform,SFT)主要套用於數位訊號處理領域,是一種離散傅立葉變換的簡化算法,其核心是基於信號具有“稀疏性”:即頻域只有小部分大值點,其餘大部分點的值趨近於0。這種算法比傳統快速傅立葉變換(Fast Fourier Transform,FFT)快10到100倍,將給數據傳輸領域帶來革命性的進步!
基本介紹
- 中文名:稀疏傅立葉變換
- 外文名:Sparse Fourier Transform(SFT)
- 別名:稀疏快速傅立葉變換(SFFT)
- 試用範圍:數位訊號處理 數據傳輸
- 提出院校:麻省理工大學(MIT)
- 提出時間:2012年
簡介,核心思想,
簡介
離散傅立葉變換(Discrete Fourier Transform,DFT)是信號處理中最基礎的理論算法之一,計算DFT最廣泛的方法是1965年由Cooley等提出的快速傅立葉變換。與直接計算DFT相比,FFT大大簡化了運算過程,可將運算量縮短1~2個數量級,推動了信號處理技術的革命性進展,被譽為二十世紀最具影響力的十大算法之一。半個世紀以來,研究人員不斷追求FFT算法的改進並提出了若干變體,如原地FFT算法和分裂基FFT算法等,這些變體在某些硬體實現上確有助益,但是複雜度並未得到明顯改觀。人們開始將目光集中在信號自身特徵上來,研究發現,大量信號具有“稀疏性”:頻域只有小部分大值點,其餘大部分點的值趨近於0。這一特徵涵蓋眾多套用領域:圖像和語音信號、機器學習理論、布爾函式分析、壓縮感知、寬頻頻譜感知等。對於這種廣泛存在且結構特殊的信號,能否實現算法性能的突破呢?
首先進行這一研究的是1993年文獻中設計的“哈達瑪變換”快速算法,不久之後又出現了一系列複數域上的研究。這些算法在一定的稀疏度範圍內,性能超越FFT ,其時間複雜度大都是由稀疏度K和lbN 構成的多項式,2012年MIT的4位研究人員提出一種更加簡單有效的算法結構,在更廣闊的適用範圍內性能超越FFT算法,重新掀起了研究的熱潮,湧現出一大批算法理論成果、代碼庫以及相關硬體設備。
核心思想
SFT算法是一種利用信號頻譜的稀疏性來降低運算複雜度的算法, 其理論框圖如圖1所示。圖中, x (n) 為長度為N的時域信號, X (k) 為x (n) 經過SFFT計算得到的頻譜。SFFT算法的核心思想是將信號的頻點按照一定規則Γ分到B個“筐”中。由於信號頻域的稀疏性, 每個“筐”中只有一個大值頻點的機率很高。對各“筐”進行頻域降採樣得到B點頻域短序列, 從中找出含大值頻點的“筐”。最後設計重構算法Γ-1恢復大值頻點在原頻譜的位置和幅值, 還原出N點原始信號頻譜。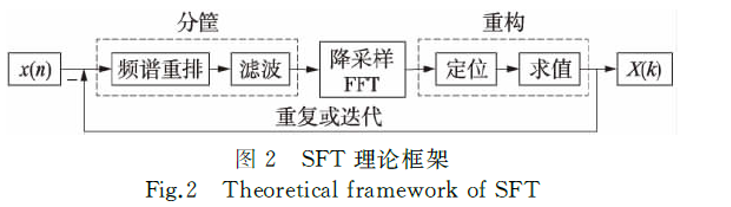

圖1