三維紊流擴散方程在空間平均化(斷面平均,垂向或橫向單獨平均)以後的簡化關係式。由於式中包含了溶質隨平均流速輸移的移流項和剪下作用產生的彌散項,故稱移流離散方程或隨流彌散方程。
基本介紹
- 中文名:移流彌散方程
- 外文名:advection-dispertionequation
- 又稱:移流離散方程、隨流彌散方程
彌散的概念,方程的一般形式,研究,
彌散的概念
由於剪下流中的流速分布(對於紊流指時均流速分布)不均與產生含有物質隨流散開的作用成為彌散或者離散(dispersion)。在移流擴散方程中,移流輸送項包含了三維流動中速度不均勻的離散影響。所以理論上可以通過求解移流擴散方程來分析,但一般難度較大。通常處理的方法是:將三維剪下流簡化為一維流或二維流,用斷面平均參數表示一維流或二維流情況,所以前述擴散問題求解中是按均勻分布流速計算的,應該考慮實際流速不均勻所造成的附加擴散,即彌散(離散)。所以彌散是由於將流場進行空間平均的簡化處理引起的。
方程的一般形式
移流彌散方程的一般形式為:
儲存量變化率=-移流輸移變化率+彌散輸移變化率-生化作用降解
當河流橫斷面積基本不變時,一維移流彌散方程為
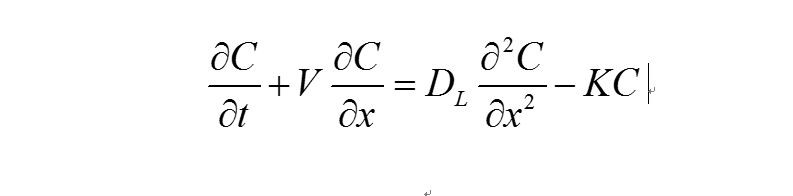
式中,C為溶質的斷面平均濃度;t為時間;V為斷面平均流速;x為橫坐標;DL為縱向離散係數;K為物質因生物化學等作用引起的動力學轉化係數。在簡單的邊界及排放條件下可求上式的解析解,在複雜的邊界及排放條件下需用數值法求解,從而獲得濃度的時空分布。

研究
1953年泰勒(G.L.Tayor)首先對圓管層流的縱向彌散問題進行了研究,1954年他又研究了圓管紊流的彌散問題。1959年J.W.埃爾德套用泰勒的方法對明槽中的彌散進行了分析。後來R.阿里斯提出了濃度矩的方法將泰勒分析彌散的方法普遍化。20世紀60年代H.B.費希爾等人推廣至天然河道的彌散計算,並研究了橫向彌散問題,認為在天然河道和港灣中橫向彌散比垂向彌散作用更重要。目前對複雜邊界及作恆定流動中的彌散已取得了一些研究成果。
當河道的平均流速比較小時,移流作用不大,彌散作用對污染物質濃度分布的影響較大,如何準確地確定彌散係數是一個重要的問題。對於過流斷面變化不大的順直河道,可根據流速分布或單寬流量的分布來計算。缺乏流速分布資料時,可選用合適的經驗公式來估算。要較準確地確定彌散係數,需進行現場示蹤試驗。
