基本介紹
- 中文名:礦物相律
- 外文名:mineralogical phase rule
- 詞性:專有名詞
- 提出時間:1911年
詳細原理,相關介紹,
詳細原理
在封閉系統中,礦物相數(P)與自由度數(F)和獨立組分數(C)之間的關係是:P+F=C+2。因為變質礦物組合一般是在一定的溫度和壓力範圍內形成的,表明變質作用通常是在溫度和壓力都可變化的條件下進行,即自由度F≥2,由此得出變質岩中平衡共生的礦物相數應等於或小於岩石中的獨立組分數,即P≤C。
這一規律稱為礦物相律,因為它是由戈爾德施密特(V.M.Goldschmidt,1911)首先提出的,又稱為戈爾德施密特礦物相律(Goldschmidt′s mineralogical phase rule)。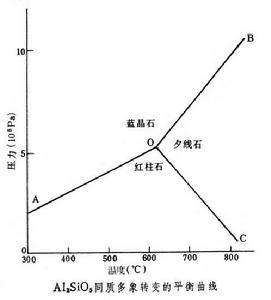 相關圖片
相關圖片
 相關圖片
相關圖片在開放體系中,岩石中的組分可分為惰性組分(Ci)和活動組分(Cm),即C=Ci+Cm,因為在一定的溫度和壓力條件下,岩石中只有惰性組分與變質岩的礦物組合有關,而完全活動組分對變質岩的礦物組合沒有影響,即自由度F≥2+Cm,由此得出變質岩中平衡共生的礦物相數應等於或小於岩石中的惰性組分數,即P≤Ci。
這一規律是由科爾任斯基(Д С Коржинский,1936年)首先提出的,因此稱為科爾任斯基礦物相律(Korzhinskiy minerological phase rule)。
相關介紹
吉布斯相律是討論平衡體系內相數、獨立組分數和自由度三者之間關係的一般規律,即在平衡條件下,組分將最大限度地形成儘可能少的相。在一般情況下,影響體系平衡狀態的因素主要是溫度和壓力。所以吉布斯相律的一般表達式為
F=C +2-P
式中 F(自由度數)為體系中獨立可變的強度因素(溫度、壓力等)的數目。它們在一定範圍內可以任意改變而不會引起相的數目的改變。
因此,自由度又稱為獨立變數。P(相數)為體系中平衡共生的相數。
岩石學中,一種礦物為一個相,固溶體礦物也算一個相,如發生了固溶體分離,則主、客晶各為一個相。C(獨立組分數)為平衡體系中組成各相所需的最小數目的獨立物質。例如:
CaCO3+SiO2=CaSiO3+CO2↑
該平衡體系由4種物質來描述:CaCO3、SiO2、CaSiO3、CO2。但其獨立組分數是3而不是4。
戈爾德施密特認為,在變質地區內,變質礦物組合是按照變質帶分布的,每一個變質帶代表一定的溫度和壓力範圍,因此由變質反應形成的礦物組合是在溫度、壓力變化的條件下進行的(即 F=2)。所以相律的一般形式為
F=C +2-P=2
又考慮到一個礦物相併非都是一種組分所組成,因而C≥P,也就是在一定溫度和壓力範圍的封閉體系內,處於穩定平衡的礦物數等於或少於岩石的獨立組分數。
例如,Al2SiO5的同質多象反應,如圖所示。當F=0時,即體系中所有強度因素都為一定值,P=1+2=3,稱為不變平衡體系,如圖中的O點;而 F=1時,體系中只有一個強度因素可以獨立變化,則P=1+1=2,稱為單變平衡,如圖中OA、OB及OC線;在F=2時,體系中的兩個強度因素都可以變化,稱為雙變平衡體系,如圖AOB、BOC、COA雙變區。

