磁感應方程是描述磁場與導電的流體發生相互作用時,磁場隨時間變化的方程,是磁流體動力學中的一個重要方程。
基本介紹
- 中文名:磁感應方程
- 外文名:Magnetic induction equation
- 學科:物理
數學表示,磁擴散效應,
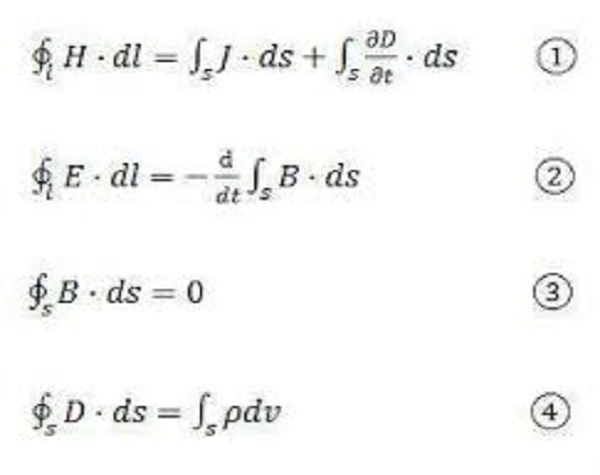
磁感應方程是描述磁場與導電的流體發生相互作用時,磁場隨時間變化的方程,是磁流體動力學中的一個重要方程。
磁感應方程是描述磁場與導電的流體發生相互作用時,磁場隨時間變化的方程,是磁流體動力學中的一個重要方程。數學表示在磁流體動力學中,電漿可以看作是良導體,由於存在洛倫茲力,歐姆定律的數學形式為:代入麥克斯韋方程組可以得到...
畢奧-薩伐爾定律適用於計算一個穩定電流所產生的磁場。這電流是連續流過一條導線的電荷,電流量不隨時間而改變,電荷不會在任意位置累積或消失。採用國際單位制,用方程表示,電流元 產生的磁感應強度為: , , 三者滿足右手螺旋關係...
提出了數值模擬對流擴散方程的新的高效和無條件穩定的數值方法,數值實驗表明對於對流占優的問題,即使套用粗格線這種方法亦不會產生非物理振盪,由於磁感應方程和Navier-Stokes方程均為對流擴散方法,因此該方法將在計算流體力學領域具有廣闊...
在一些情況下,由倫敦方程我們可以得到超導體內磁感應強度的方程:由上述關係式定義london穿透深度λ= ,其中α= 穿透深度的物理意義是超導體內部磁感應強度在穿透深度λ處衰減到表面數值的 。理論缺陷 1.無法解釋穿透深度隨著外界變數...
矢量磁位 對於恆定磁場,由於▽·B=0(B的散度處處為0),因此,磁感應強度可以表示為另一矢量場的旋度,即 上式中的矢量場A是矢量磁位.它滿足方程 與電流密度的積分關係為 當電流體密度已知時,可以直接用比奧薩伐定律通過積分計算...
