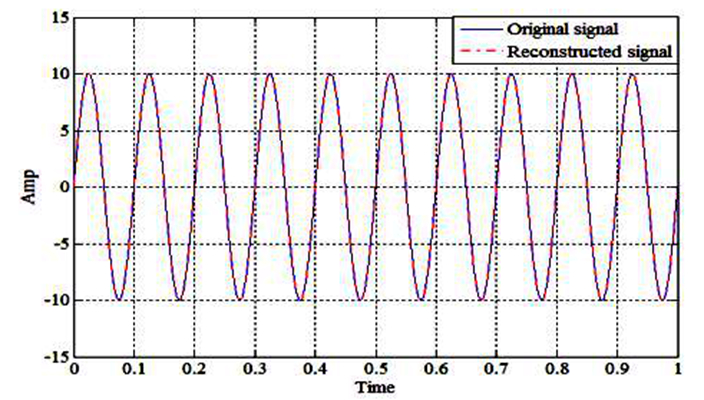
短時傅立葉變換(STFT,short-time Fourier transform,或 short-term Fourier transform))是和傅立葉變換相關的一種數學變換,用以確定時變信號其局部區域正弦波的頻率與相位。
基本介紹
- 中文名:短時傅立葉變換
- 外文名:STFT,short-time Fourier transform,或 short-term Fourier transform
- 相關學科:數學
- 相關變換:傅立葉變換
它的思想是:選擇一個時頻局部化的窗函式,假定分析窗函式g(t)在一個短時間間隔內是平穩(偽平穩)的,移動窗函式,使f(t)g(t)在不同的有限時間寬度內是平穩信號,從而計算出各個不同時刻的功率譜。短時傅立葉變換使用一個固定的窗函式,窗函式一旦確定了以後,其形狀就不再發生改變,短時傅立葉變換的解析度也就確定了。如果要改變解析度,則需要重新選擇窗函式。短時傅立葉變換用來分析分段平穩信號或者近似平穩信號猶可,但是對於非平穩信號,當信號變化劇烈時,要求窗函式有較高的時間解析度;而波形變化比較平緩的時刻,主要是低頻 信號,則要求窗函式有較高的頻率解析度。短時傅立葉變換不能兼顧頻率與時間解析度的需求。短時傅立葉變換窗函式受到W.Heisenberg不確定準則的限制,時頻窗的面積不小於2。這也就從另一個側面說明了短時傅立葉變換窗函式的時間與頻率解析度不能同時達到最優。