相對論宇宙學

在愛因斯坦的引力理論和相對論力學的基礎上建立起來的宇宙理論。它的一些基本結論都是根據所謂宇宙學原理(即宇宙物質在大尺度上具有均勻各向同性)的假定而推得的。

相對論宇宙學

在這種宇宙理論中，空間各點的曲率處處相同，但彎曲程度可以隨時間變化（不改變其正負號）。其中正曲率（空間曲率署符k=+1）對應於一個沒有邊界、但體積有限的閉合宇宙；零曲率 (k=0)對應於一個平直的開放宇宙；負曲率(k=-1)則對應於一個雙曲型的開放宇宙。宇宙的膨脹或收縮運動在所有方向上是一樣的，它可以由度規公式中的宇宙標度因子 R=R(t)來描述。R隨宇宙時t的相對變化率就是哈勃常數，即H=凟/R。知道了R隨時間的變化，也就知道了宇宙的歷史和發展趨向。假定星系可以構想為均勻而靜止地分布在整個空間中，那么就可用理想流體的能量－動量張量來描述它們。這時，根據引力場方程，就能推出均勻各向同性宇宙學模型的動力學方程：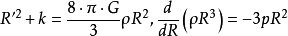

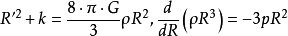
式中G為引力常數。給定物態方程的壓力p=p(ρ),可求得函式R(t)，詳細分析R(t)的性質，就得到各種典型的相對論宇宙模型。