直接前元(immediate predecessor)是一種特殊相關的元素，它是偏序集中某元素的前元，並且該元素的一切其他前元也是它的前元。設〈A，R〉為偏序集。若a，b∈A，a≠b，aRb，並且對於任何c∈A，當aRc且cRb時，有a=c或c=b，則a稱為b的直接前元，b稱為a的直接繼元。如果a的直接繼元存在且惟一，可記為a或S(a)。A中元素不一定有直接前元(繼元)，也可能有一個或多個。
基本介紹
- 中文名：直接前元
- 外文名：immediate predecessor
- 所屬學科：數學（離散數學）
- 簡介：偏序集中某元素的前元
基本介紹,相關介紹,
基本介紹
集合S上的一個關係“
”如果有下列三個性質：
(1)自反性：對於S的每一個a,a a；
(2)反對稱性：若a b且b a，則a=b；
(3)傳遞性：若a b且b c，則a≤c，
a
b(讀作“a嚴格前於b")：若a b但a≠b；
a
b(讀作“a後於b"(“a在b之後")；
a
b(讀作“a嚴格後於b")：若ba。
若S的元素a和b既不是a b又不是b a，它們是不可比較的。如果S的元素a嚴格在b之前，即a b，並且不存在S的元素x使得a x b，那么我們說a是b的一個直接前元，記作a
b或
。關於偏序集以及直接前元等，有多種不同的記法。在下面哈塞(Hasse)圖表示的偏序集中，a有三個直接前元，它們互不能比較;a又有兩個直接繼元.b有五個前元，一個直接前元，而無繼元.e，f，h都無前元，而e，f都以a為直接繼元，h以g為直接繼元.A中元素也可能有前元(繼元)而無直接前元(直接繼元)，例如，當A為實數集，R為小於關係時，A中任何一個元素都無直接前元與直接繼元。
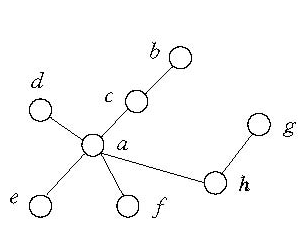圖1 Hasse圖相關介紹
設S是一個偏序集，且a,b屬於S，我們說a是b的一個直接前元或b是a的一個直接繼元，或者b蓋住a，記作
假定S是有限偏序集，S中的序將完全清楚，如果我們知道S中所有 的元素對a,b，則知道S上的
美系。這是因內x<y當且仗當x y或在S中存在元素
使得
有限偏序集S的Hasse圖是直接圖解，它的頂點是S的元素，從a到b有一個有向邊，當a<b時， (我們不畫一個從a指向b的箭頭，而是將b置於高於a的地方，然後畫一線將它們連起來，很清楚，向上運功引起後元)。因此在圖中，從點x到點y有一有向路，若且唯若x<y。同祥，在S的圖中沒有環，因為序關係是反對稱的。
偏序集S的Hasse圖對描述S中元素的類型很有用，有時我們利用給出其Hasse圖來定義一個偏序集。注意偏序集S的Hasse圖不需要連通。
例如，設A={1,2,3,4,6,8,9,12,18,24}是在“x整除y”關係下的序集，A的Hasse圖由圖2中給出。(在偏序集的Hasse圖中，線的方向總是向上)。
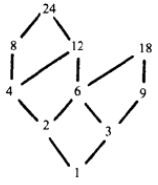圖2