盆地流體模擬是指以盆地動力學背景、構造、沉積充填、熱史綜合作用為基礎再現盆地演化過程中流體活動規律，包括盆地演化過程中沉積物物性、溫度場、壓力場。進而可為盆地內油氣運移和聚集、成礦流體運移和聚集提供依據。
基本介紹
- 中文名：盆地流體模擬
- 外文名：Basin fluid simulation
- 基本方法：解析方法、數值方法
- 基礎：動力學背景、構造、沉積充填
- 目的：再現盆地演化過程中流體活動規律
- 套用：吻合關係較好
背景,盆地流體活動的基本原理,基本模型,基本方法,套用分析,
背景
盆地流勸習殼體流動是盆地動力學背景、構造、沉積充填、熱史綜合作用的結果(Garven，1989，1995)。盆地流體模擬的目的就是要再現盆地演化過程中流體活動規律，包括盆地演化過程中沉積物物性、溫度場、壓力場以及流體流動速度、流量、水 -岩相互作用速率等參數隨時間的變化(Bethke等，2001)，進而可為盆地內油氣運移和聚集、成礦流體運移和聚集提供依據。因此，盆地流體模擬是成礦流體或油氣運聚模擬的基礎(康永尚等，1999;解習農等，2003)，也是盆地內地質資源評價中必不可少的一個環節。
盆地流體活動的基本原理
盆地流體活動雖然錯綜複雜，但它總是遵循兩條基本原理，即流體活動過程中的質量守恆和 能量守恆定律。下面介紹盆地流 體模擬過程所 遵循的基 本原理。
(一)達西定律
法國工程師 H.Darcy在 1856年發表了水通過直立均質砂粒滲濾管的實驗結果，結果表明流體滲濾速度總是與測壓管水柱高差和滲流係數成正比，即：
式中，v為流體滲流速度(cm/s);Q為單位時間內流體滲濾過濾管的體積量，或流量(cm /s);A為催愚紙希管道橫截面積(cm );Δh為測壓管水柱高差(cm);Δh/L為水力梯度(cm/cm);K為水力傳導係數，即滲流係數。
（二）質量守恆定律
當流體通過孔隙介質內一個截面時，在任一時間間隔內從這個截面流出的質量等於向這個截面流入的質量，即所謂連續性方程。
（三）溶解物質質量守恆定律
盆地流體分子濃度擴散可表述戰付達為：
式中，D為擴散係數;Dw 為水動力熱擴散係數;Ds 為分子擴散係數;
C為濃度差。
基本模型
盆地流體流動過程既包括水動力過程，也包括熱傳導過程和溶質運移過程：
1.水動力模型
根據達西定律，盆地流體流動受壓力差的驅動，單位體積的流速可表述為：
Pex是剩餘孔隙壓力，即流體壓力與靜水壓力之差。
2.熱動力模型
盆地流體流動過程擴散既包括隨流熱擴散和岩石熱傳導，有時還有新生熱源，如由放射性元素所產生的單位體積的產熱量，表達式為：
式中：Cb為骨架岩石的特徵熱;Cw 為孔隙流體的特徵熱;Kb 為骨架岩石的熱傳導係數;Qt 是由放射性元素所產生的單位體積的產熱量。
3.溶質運移模型
盆地流體中化學物質運移既包括水動力擴散，也包括由分子振動使物質從高濃度向低濃度的擴散作用，其表達式為：
式中：u為流體的孔隙 平均流速(m/L);D為水動力彌散係數 m/L;D=D″+D′，D′為機械謎嘗仔彌散係數，D′=αu，α為彌散度(dispersivity)，D″為多孔介質分子擴散係數;I為源匯項。
基本方法
盆地流體模擬的方法有兩種：一種是用解析方法，另一種是數值方法。前者就是用數學上的積分法或積分變換等方法直接求數學模型的解，它是數學模型的精確解；後者則是用離散化的方法求解數學模型，其解為數值的集合，是數學模型的近似解。在盆地流體模擬中，由於流體活動發生於一個非均質的複雜地層系統之中，用解析方法必須對於研究對象做出各種假設條件，例如假設地層是均質的，邊界是簡單的幾何形狀等等，這種解析解的結果可以簡單明了的看出盆地流體運動的一般規律。然而，沉積盆地是十分複雜的，用解析方法所做的一些簡單假設不能完全反映葛她榆地層的真實情況，如各向異性、特殊邊界情況、盆地演化過程中的不規律性變化現象等。使用數值方法求解數學模型，恰好彌補了解析方法的不足，它通常是將研究範圍離散化，也就是進行格線剖分，然後將模擬區域的格線方程聯合求解，進而得出數值解的集合（陳崇希等，1990）。因此，數值方法成為盆地流悼才謎和體定量模擬中最重要的方法。
數值方法求解數學模型的方法有兩種，一種是有限差分法，另一種方法是有限元法。這兩種方法最大區別在於有限元法可以更好地模擬複雜的邊界條件，用各種形狀（一般為三角形）的格線單元最大可能地逼近模擬邊界，所以一般用於那些邊界影響比較大的問題的求解；而有限差分法可以很順利地建立差分方程，在精度允許的範圍內採用簡單的格線系統將模擬區域離散化，此外有限差分法的求解更為簡單一些。
套用分析
盆地流體模擬的套用已在國內外有許多報導，許多學者都試圖從盆地水動力歸謎學過程來探討盆地流體活動與油氣運移、聚集 的成因聯繫(Ungereretal.，1990;Bethkeetal.，1991;Gvirtzman& Stanislavsky，2000;Lee& Williams，2000;Xieetal.，2001，2003)。盆地流體既是油氣運移、聚集的載體，也是其他成礦流體的載體，所模擬的古水動力場及演化特徵可以作為其他模擬研究的基礎，比如油氣成藏動力學模擬、與地下水活動相關的生物作用過程模擬等。下面以松遼盆地十屋斷陷的實例模擬作一介紹。
(一)模型參數的獲取
盆地流體數值模擬方法需要地質、地球物理、地球化學、熱力學、岩石物理學以及流體力學等多方面的各種參數，這些參數的正確選取直接關係到模擬結果的可信度。這些模型參數包括地質參數、岩石物理學參數和流體力學參數。
地質參數包括沉積地層地質年代、厚度、岩性、古水深、古地表溫度、古熱流、地溫梯度、沉積相以及盆地演化過程中的地質事件等內容。有些參數可以通過鑽井、地震資料和測試資料獲取。
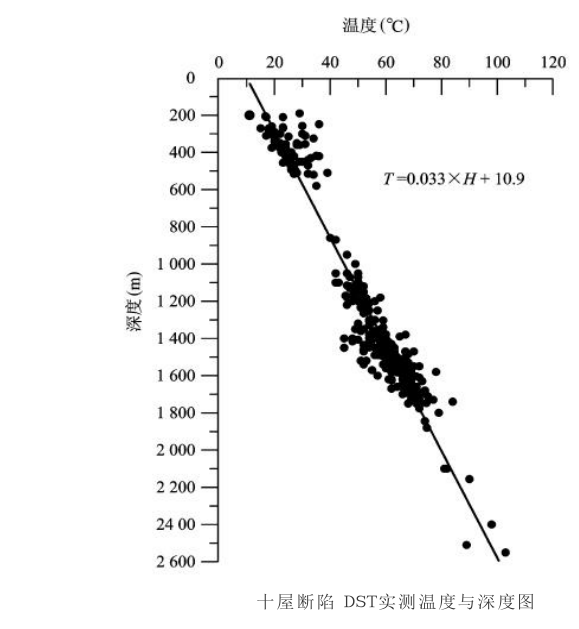
需要說明的是盆地演化過程中古地溫和地溫梯度可能是變化的，因此在盆地流體模擬中需要獲取不同地質時期的古地表溫度和古地溫梯度。比如，在十屋斷陷實例的模擬中就採用了不同的地熱資料，即裂陷期的古熱流值為 2.9HFU，裂後期為 1.95HFU，現今熱流值為 1.55HFU。岩石物理學參數包括密度、孔隙度、滲透率及其壓縮係數、熱導率、熱容(即比熱)和熱膨脹係數等。
流體力學參數主要包括流體密度、黏度、壓縮係數與膨脹係數、飽和度、溶解度、體積係數以及氣體擴散係數等。多數流體力學參數如流體密度、黏度、溶解度等隨溫度和壓力的變化而變化。
(二)模擬結果分析
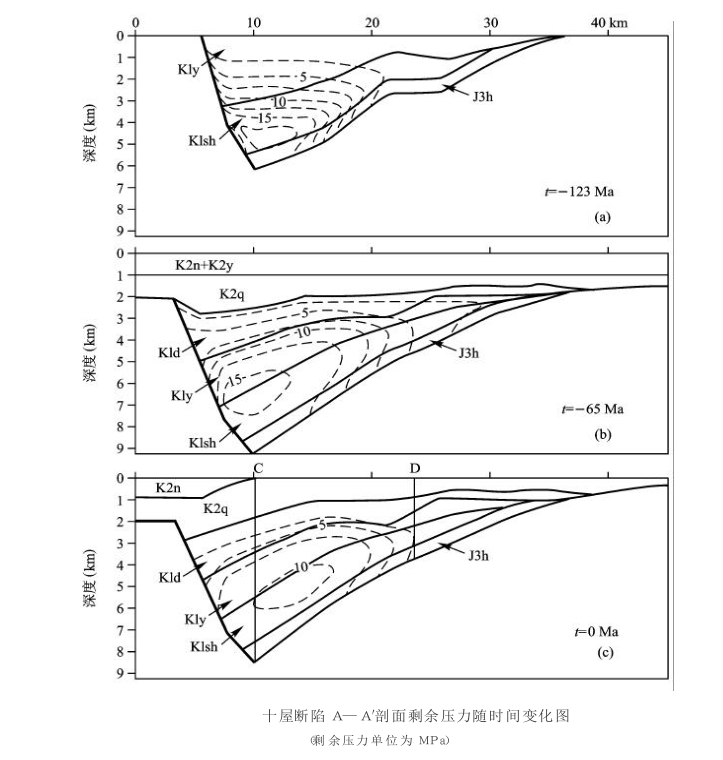
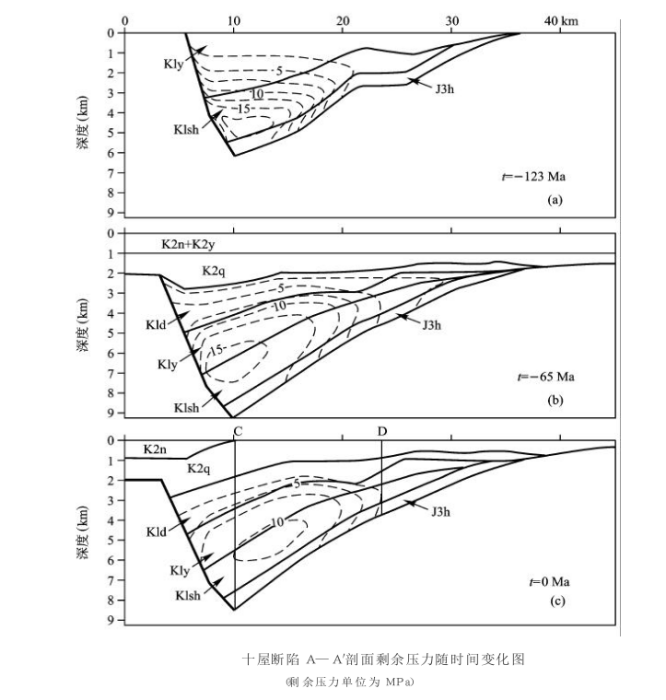
選擇通過十屋斷陷的 NE向剖面，通過數值模擬揭示了盆地演化過程中溫度場、壓力場和流體流速等變化情況。模擬結果與鑽井實測的溫度和 Ro 具有很好的吻合關係。
模擬結果表明：十屋斷陷地層壓力體系經歷了從異常高壓向異常低壓的演變過程。營城子組沉積期末在斷陷中央已出現異常高壓，至登婁庫組沉積期末，異常壓力變大，其範圍也變大。該區異常高壓形成可能與裂陷期快速沉降速率有關，凹陷中央沙河子組和營城子組沉積速率達 200m/Ma以上。進入裂後期，由於沉積速率較低，一般小於 100m/Ma，至晚白堊世青山口組、姚家組和嫩江組沉積期其沉積速率小於 50m/Ma，斷陷內異常超壓減小，但仍表現為高的剩餘壓力。直到進入新生代地層抬升剝蝕期，地層壓力逐漸從異常高壓轉變為異常低壓。
數值方法求解數學模型的方法有兩種，一種是有限差分法，另一種方法是有限元法。這兩種方法最大區別在於有限元法可以更好地模擬複雜的邊界條件，用各種形狀（一般為三角形）的格線單元最大可能地逼近模擬邊界，所以一般用於那些邊界影響比較大的問題的求解；而有限差分法可以很順利地建立差分方程，在精度允許的範圍內採用簡單的格線系統將模擬區域離散化，此外有限差分法的求解更為簡單一些。
套用分析
盆地流體模擬的套用已在國內外有許多報導，許多學者都試圖從盆地水動力學過程來探討盆地流體活動與油氣運移、聚集 的成因聯繫(Ungereretal.，1990;Bethkeetal.，1991;Gvirtzman& Stanislavsky，2000;Lee& Williams，2000;Xieetal.，2001，2003)。盆地流體既是油氣運移、聚集的載體，也是其他成礦流體的載體，所模擬的古水動力場及演化特徵可以作為其他模擬研究的基礎，比如油氣成藏動力學模擬、與地下水活動相關的生物作用過程模擬等。下面以松遼盆地十屋斷陷的實例模擬作一介紹。
(一)模型參數的獲取
盆地流體數值模擬方法需要地質、地球物理、地球化學、熱力學、岩石物理學以及流體力學等多方面的各種參數，這些參數的正確選取直接關係到模擬結果的可信度。這些模型參數包括地質參數、岩石物理學參數和流體力學參數。
地質參數包括沉積地層地質年代、厚度、岩性、古水深、古地表溫度、古熱流、地溫梯度、沉積相以及盆地演化過程中的地質事件等內容。有些參數可以通過鑽井、地震資料和測試資料獲取。
需要說明的是盆地演化過程中古地溫和地溫梯度可能是變化的，因此在盆地流體模擬中需要獲取不同地質時期的古地表溫度和古地溫梯度。比如，在十屋斷陷實例的模擬中就採用了不同的地熱資料，即裂陷期的古熱流值為 2.9HFU，裂後期為 1.95HFU，現今熱流值為 1.55HFU。岩石物理學參數包括密度、孔隙度、滲透率及其壓縮係數、熱導率、熱容(即比熱)和熱膨脹係數等。
流體力學參數主要包括流體密度、黏度、壓縮係數與膨脹係數、飽和度、溶解度、體積係數以及氣體擴散係數等。多數流體力學參數如流體密度、黏度、溶解度等隨溫度和壓力的變化而變化。
(二)模擬結果分析
選擇通過十屋斷陷的 NE向剖面，通過數值模擬揭示了盆地演化過程中溫度場、壓力場和流體流速等變化情況。模擬結果與鑽井實測的溫度和 Ro 具有很好的吻合關係。
模擬結果表明：十屋斷陷地層壓力體系經歷了從異常高壓向異常低壓的演變過程。營城子組沉積期末在斷陷中央已出現異常高壓，至登婁庫組沉積期末，異常壓力變大，其範圍也變大。該區異常高壓形成可能與裂陷期快速沉降速率有關，凹陷中央沙河子組和營城子組沉積速率達 200m/Ma以上。進入裂後期，由於沉積速率較低，一般小於 100m/Ma，至晚白堊世青山口組、姚家組和嫩江組沉積期其沉積速率小於 50m/Ma，斷陷內異常超壓減小，但仍表現為高的剩餘壓力。直到進入新生代地層抬升剝蝕期，地層壓力逐漸從異常高壓轉變為異常低壓。
