疊式存儲算法(stack algorithm)又稱堆疊算法，疊式存儲算法的思想很簡單，它的序列解碼的基本概念明顯易懂。解碼器由一種編排好的表格或稱堆疊組成。在堆疊內，把已探尋過的路徑，按其對數似然值的降序排列好。堆疊頂端存儲著該堆疊全部存儲路徑中最大對數似然函式的路徑。由於該路徑與正確路徑最相似，所以，它是下一步被研究的對象(每深入一級，延伸出兩條支路)。隨著每次延伸之後，堆疊就重新排列一次。其結果是，哪一條路徑的對數似然函式增大，那它就是下一步被繼續研究的對象。如果該路徑的對數似然函式減小，那么，它就要從頂端位置落下，並儲存在堆疊適當的位置上，從而得到一個新的頂端節點。把每一條已探明的路徑用其最終的節點來表示，則堆疊便可等效地看成是一張節點目錄表，而節點則是按其對數似然函式值排列的。這樣，解碼器的目的就是尋求頂端節點，再延伸其後繼節點，然後對堆疊作適當重新排列。當把起始原節點裝入堆疊後，此節點的對數似然函式就取為零。解碼算法包括下列步驟：1．計算其頂端節點的全部後繼節點的對數似然函式，並在堆疊適當的位置上把新的路徑存進去。2．當節點的後繼節點一旦被存入堆疊後，該節點便在堆疊上被消除。3．如果新的頂端節點是最後節點，則運算停止或轉回到第1級上去。當運算從迴路系統中逸出時，頂端節點就是解碼所得路徑的端節點。於是，整個解碼路徑就很容易從堆疊所存儲的信息中求得。
基本介紹
- 中文名：疊式存儲算法
- 外文名：stack algorithm
- 別名：堆疊算法，堆疊存儲解碼，ZJ算法
- 提出人：扎崗基洛夫，傑里涅克
- 相關概念：費諾算法
- 類型：堆疊算法
基本介紹,算法步驟,疊式存儲算法的特點,
基本介紹
疊式存儲解碼(或稱堆疊存儲解碼)法是序列解碼方法的一種，是扎崗基洛夫和傑里涅克於1966年和1969年分別獨立地發現這種算法，簡稱ZJ算法。這種算法依然是根據費諾度量，解碼器在碼樹上尋找正確路徑時，力求儘早地排除所有的非最大似然路徑，從而使解碼器的平均計算量減少。
在疊式解碼算法中，有一個大容量的存儲器，或稱之為疊式存儲器(以下簡稱：SS)，用來存儲被比較的不同長度的路徑及其路徑值。在解碼過程中的每一步(每比較、計算一次)，把具有最大路徑值的路徑及其度量值存入SS最上一行(第一行)，其它的以度量值遞減的次序，將其路徑和度量依次存放在SS中。當解碼進行到下一步時，解碼器計算存放在SS中第一行路徑的後續20個分支的度量值，並與存儲在第一行的度量值相加，從而得到20個新的度量值，並且把這些新的度量值與SS中其它行的度量值進行比較，根據比較結果，按照度量值的大小重新排列，把具有最大度量值的路徑及其量值放在SS中第一行，取代了原來存放在第一行的內容，其餘的按度量值遞減的次序捧列。當解碼進行到某一步後，若SS中第一行的路徑已達到碼樹的終端節點(第
階節點)，則解碼完畢，解碼器輸出SS中的第一行路徑作為判決路徑輸出。因此，疊式解碼算法所判決的路徑是具有最大似然函式的路徑。
算法步驟
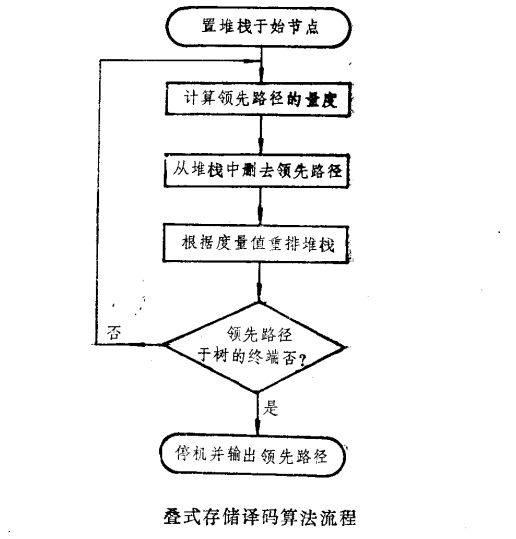
疊式存儲算法包括下列步驟：
1．從碼樹的起始節點(第0階節點)開始解碼，SS中全部為零。
2．計算存在SS第一行的路徑後續各分支的度量值，並與原來存儲的度量值相加。
3．刪去SS第一行原存儲的內容。
4．挑選一條有最大度量值的路徑存入SS的第一行。若有一條以上的路徑具有最大度量值，則任選一條，並且按度量值遞減的次序，重新排列SS中的次序和內容。
5．若SS中第一行的路徑已處在碼樹的終點，則中止解碼。否則回到第二步。
6．解碼完畢後，解碼器把第一行的內容輸出給用戶。
疊式存儲算法的特點
疊式存儲算法有如下特點：
1．與費諾算法相同，解碼器譯每一幀(L段)接收序列的計算次數，隨信道干擾的大小而變化，若干擾嚴重，錯誤個數增加，則計算次數加大，反之則減少，平均計算次數也與m無關，因此可以選用大m也就是自由距離大的碼，從而使誤碼率做的很小。
2．需要大容量的存儲器。因為每譯一步，就要有(20－1)組數據存入到SS存儲器。
3．也必須有一個輸入快取器，存儲輸入給解碼器的接收序列，以便在解碼過程中從一個節點跳向另一個節點時，使用以前的碼段，以及存儲此時刻後的接收碼段。如費諾算法一樣，在干擾嚴重情況下，解碼器搜尋時間很長，也可能引起解碼器溢出。一般，當發生溢出時，應向用戶發出告警信號，表示這一幀信號有誤，或者，在有反饋信道情況下，經反饋信道要求發端重發。
4．有比費諾算法較高的解碼速度，但需要SS存儲器。由於費諾算法不需要SS存儲器，而且也能達到比較高的解碼速度，所以在實用中，費諾算法要比疊式存儲算法套用的廣泛。
