對於由一平面截一圓錐面所得到的圓錐曲線,切於該平面並且沿一個圓周切於該圓錐面的球面,稱為所給圓錐曲線的當德蘭球。對於拋物線,只有一個當德蘭球;對於橢圓和雙曲線,則有兩個當德蘭球。當德蘭球與所給平面的切點是圓錐曲線的焦點。
基本介紹
- 中文名:當德蘭球
- 外文名:Dandelin sphere
- 適用範圍:數理科學
簡介
數量
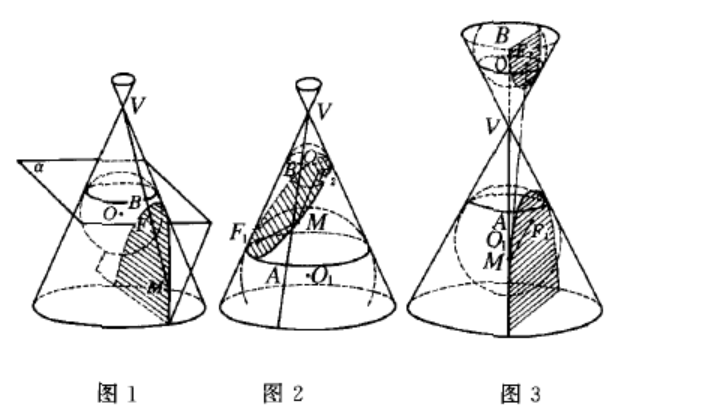 圖1
圖1對於由一平面截一圓錐面所得到的圓錐曲線,切於該平面並且沿一個圓周切於該圓錐面的球面,稱為所給圓錐曲線的當德蘭球。對於拋物線,只有一個當德蘭球;對於橢圓和雙曲線,則有兩個當德蘭球。當德蘭球與所給平面的切點是圓錐曲線的焦點。
 圖1
圖1對於由一平面截一圓錐面所得到的圓錐曲線,切於該平面並且沿一個圓周切於該圓錐面的球面,稱為所給圓錐曲線的當德蘭球。對於拋物線,只有一個當德蘭球;對於橢圓和...
華斯蘭德足球俱樂部球隊資料 編輯 名字:華斯蘭德足球俱樂部英文名:Waasland-Beveren 國語譯名:華斯蘭德足球俱樂部所屬國家:比利時 聯賽級別:比乙華斯蘭德足球俱樂部...
英文名:Waasland-Beveren 國語譯名:華斯蘭德貝弗倫足球俱樂部所屬國家:比利時 聯賽級別:比利時甲級聯賽華斯蘭德貝弗倫足球俱樂部球隊陣容 編輯 ...
威文·斯蒂蘭德,1970年生,美國人,籃球運動員,畢業於聖迭戈大學。...... 威文·斯蒂蘭德,1970年生,美國人,籃球運動...關鍵是他帶來了炫目華麗的美式球風,他的...
德蘭萊,足球運動員,1992年5月14日出生於挪威斯塔萬格。...... 德蘭萊,足球運動員,1992年5月14日出生於挪威...歐洲冠軍聯賽:出場0次,進0球德蘭萊職業生涯 ...
梅德蘭是出生於1980-12-28的阿根廷足球運動員。...... 梅德蘭是出生於1980-12-28的阿根廷足球運動員。...歐洲冠軍聯賽:出場0次,進0球梅德蘭職業生涯 編輯 ...
霍夫蘭德早在效力埃因霍溫的時候就有著很高的評價,04年從埃因霍溫轉會沃爾夫斯堡,並且擔任球隊隊長。07年霍夫蘭德轉會到費耶諾德,幫助球隊奪得荷蘭杯冠軍。...
梅德蘭出道於皇家馬德里青訓,2014年進入皇馬B隊,同年完成一線隊首秀並打入歐冠處子球。2015年7月被租借至赫塔菲。 2016年7月11日,梅德蘭轉會至瓦倫西亞,雙方簽約...
代表國家隊:出場0次,進0球歐洲三大杯:出場0次,進0球歐洲冠軍聯賽:出場0次,進0球范德文職業生涯 編輯 賽季 俱樂部 號碼 出場 進球 國家 聯賽等級 排名 2007...
當時赫爾蒙德的前身赫爾蒙迪亞55俱樂部破產,赫爾蒙德在他的基礎上重新建立起來。歷史上赫爾蒙德在1982年獲得過一次荷乙聯賽冠軍,並在1985年闖入了荷蘭杯決賽,可惜...
德古茲曼兩年間在英超聯賽中出場71次,攻入9球,隨隊獲得2013聯賽杯冠軍。喬納森·德·古茲曼加盟那不勒斯 2014年8月20日,意甲勁旅那不勒斯官方宣布,德古茲曼正式成為...
