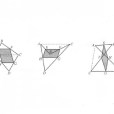
瓦里尼翁平行四邊形(Varignon parallelogram)是四邊形的一個特殊內接四邊形。順次連結四邊形各邊中點而成的四邊形是平行四邊形,稱為瓦里尼翁平行四邊形。它的面積是原四邊形面積的一半,這個平行四邊形是瓦里尼翁(P.Varignon)發現的,但遲至1731年才發表。
基本介紹
- 中文名:瓦里尼翁平行四邊形
- 外文名:Varignon parallelogram
- 所屬學科:數學
- 所屬問題:平面幾何(平行四邊形)
- 發現者:瓦里尼翁(P.Varignon)
- 別稱:中點四邊形
基本介紹,Varignon平行四邊形的證明與推廣,Varignon平行四邊形的面積,
基本介紹
定理依次連結四邊形各邊中點的圖形是平行四邊形(P.Varignon,1654-1722,法國)。
定理也體現數學和諧之美,推導也很簡單,用三角形的中位線定理即可,但是令人感到驚奇的是此定理遲至1721年才發現,定理對於凹四邊形(圖a(a)),交叉四邊形(圖1(b)),有一點不在另外三點平面上的空間四邊形(圖1(c))都成立,這種平行四邊形都稱為Varignon平行四邊形(也叫“中點四邊形”)。
Varignon平行四邊形的證明與推廣
如圖2:順次連結四邊形ABCD各邊的中點E、F、G、H所得的四邊形EFGH平行四邊形。
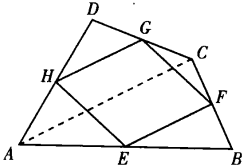 圖2
圖2證明連結AC
因為:E、F分別為AB、BC的中點
所以:EF是△ABC中位線
所以:EF//AC且EF=1/2AC
同理可證明:
HG//AC且HG=1/2AC
所以:EF//HG且EF=HG
所以:四邊形EFGH是平行四邊形。
其實,這個例題也可以連結肋來證明EH與FG平行且相等,就可以證明四邊形EFGH是平行四邊形。(如圖3)
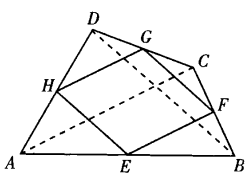 圖3
圖3從圖形可以看出,要想判定中點四邊形EFGH的形狀,其實只要判定原四邊形ABCD的對角線AC與肋的關係,是相等,還是垂直,或是二者皆有。
易證明:
若AC=BD,可推出四邊形EFGH的四條邊都相等,則四邊形EFGH是菱形。
若AC⊥BD,可推出四邊形EFGH的四個角都是90度,則四邊形EFGH是矩形。
若AC=BD且AC⊥BD,可推出四邊形EFGH的四條邊都相等,四個角都是90度,則四邊形EFGH是正方形。
歸納結論:任意四邊形的中點四邊形是平行四邊形;若四邊形的對角線相等,則它的中點四邊形是菱形;若四邊形的對角線垂直,則它的中點四邊形是矩形;若四邊形的對角線垂直且相等,則它的中點四邊形是正方形。
Varignon平行四邊形的面積
(如圖4)只要作△ACD的高DM,DM交AC於M,易知DM的一-半是平行四邊形GHIJ的高。
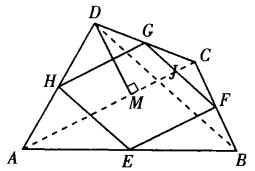 圖4
圖4分析:易知AC=2HG
所以△ACD的面積



=2平行四邊形GHIJ的面積
同理可證明:
△ABC的面積=2平行四邊形EFIJ的面積
以上兩式相加可得:
四邊形ABCD的面積=2四邊形EFGH的面積
歸納結論:中點四邊形的面積是原四邊形面積的一半。