瓦爾克爾氏預測法

瓦爾克爾氏預測法

瓦爾克爾氏預測法（瓦爾克爾氏自身身高預測法），是一個較為簡便的預測最終身高的方法，這個方法是利用兒童少年某一時期的身高來預測未來的最終身高，或是以兩個時期的身高進行比較後得出最終身高。

該方法有一定的可靠性，被廣泛運用於身高預測中。此法共分為一次預測法及兩次預測法。

概述,預測方法,一次預測法,兩次預測法,

概述

很多家長和兒童希望了解自己孩子的未來身高情況，運動員的身高是影響到一些運動項目成績的關鍵因素，如：跳高、籃球等。

預測方法

一次預測法

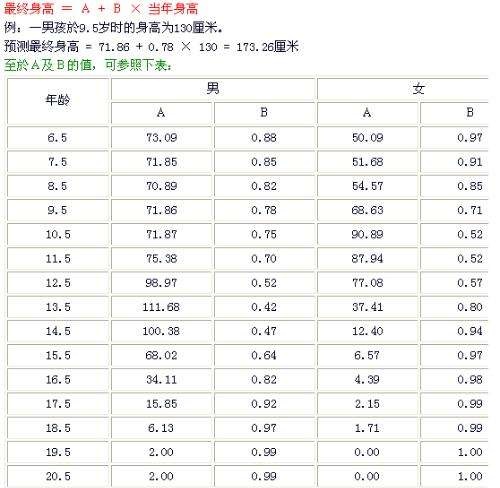
最終身高 = A + B × 當年身高
例：一男孩9.5歲時的身高為130厘米。
預測最終身高 = 71.86 + 0.78 × 130 = 173.26厘米
A及B的值，可參照下表進行計算：
年齡
男
女
A
B
A
B
6.5
73.09
0.88
50.09
0.97
7.5
71.85
0.85
51.68
0.91
8.5
70.89
0.82
54.57
0.85
9.5
71.86
0.78
68.63
0.71
10.5
71.87
0.75
90.89
0.52
11.5
75.38
0.70
87.94
0.52
12.5
98.97
0.52
77.08
0.57
13.5
111.68
0.42
37.41
0.80
14.5
100.38
0.47
12.40
0.94
15.5
68.02
0.64
6.57
0.97
16.5
34.11
0.82
4.39
0.98
17.5
15.85
0.92
2.15
0.99
18.5
6.13
0.97
1.71
0.99
19.5
2.00
0.99
0.00
1.00
20.5
2.00
0.99
0.00
1.00

兩次預測法

最終身高= A + B1 × 當年身高 + B2 × (第一、二次身高差 ÷ 間隔月數）
例：一男孩9.5歲，第一次測量身高為130厘米，八個月後再測身高為132.4厘米。
預測最終身高 = 70.85 + 0.8 × 130 + (-0.3) × [(132.4 - 130) ÷ 8] = 173.95厘米
A，B1及B2的值，可參照下表進行計算：
年齡
男
女
A
B1
B2
A
B1
B2
6.5
75.40
0.84
0.35
44.23
1.03
-0.20
7.5
74.31
0.82
0.25
49.10
0.94
-0.20
8.5
72.24
0.81
-0.03
53.25
0.86
-0.05
9.5
70.85
0.80
-0.30
63.34
0.76
-0.25
10.5
68.04
0.80
-0.65
73.07
0.69
-1.05
11.5
65.47
0.81
-1.20
76.71
0.63
-0.75
12.5
63.90
0.81
-1.65
73.93
0.58
0.20
13.5
99.03
0.54
-0.95
31.16
0.81
0.95
14.5
101.71
0.44
0.50
14.56
0.92
0.50
15.5
53.40
0.70
0.75
6.32
0.97
0.25
16.5
21.92
0.88
0.60
4.39
0.98
0.00
17.5
14.67
0.92
0.40
2.15
0.99
0.00
18.5
7.80
0.96
0.25
1.71
0.99
0.00
19.5
3.70
0.98
0.15
0.00
1.00
0.00
20.5
1.84
0.99
0.10
0.00
1.00
0.00
兩次預測法必須在第一次測量當年身高后，在相隔八至十五個月內複查第二次身高。由於兩次預測法包含動態變化的因素，所以其可靠性較一次預測法高。
更多關於身高和身高預測的內容，請點擊身高詞條

相關詞條

熱門詞條

聯絡我們