如果作用在一力學體系上諸約束反力在任意虛位移δr中所作的虛功之和為零,那么這種約束叫做理想約束。理想約束的概念是從實際約束中抽象得來,它反映了相當廣泛的一些實際約束的主要性質。
基本介紹
- 中文名:理想約束
- 外文名:ideal constraint
- 定義:所有約束力所做的虛功之和為0
- 常見情況:光滑接觸面約束、光滑鉸鏈
- 相關定義:虛功、虛位移
- 套用學科:理論力學
定義,幾種常見情況,光滑接觸面約束,無重剛桿約束,連線兩剛體的光滑鉸鏈約束,不可伸長的繩索,無滑動的滾動,研究意義,
定義
根據約束力作實功等於零,常見的光滑固定面約束、光滑鉸鏈、無重剛桿、不可伸長的柔索、固定鉸鏈支座、滾動支座、固定端等約束均為理想約束,現從虛功角度看,這些約束仍然為理想約束。另外,由於固定粗糙平面約束力對純滾動剛體所做的實功與虛功均為零,也可認為粗糙平面對純滾動的約束為理想約束。
幾種常見情況
光滑接觸面約束
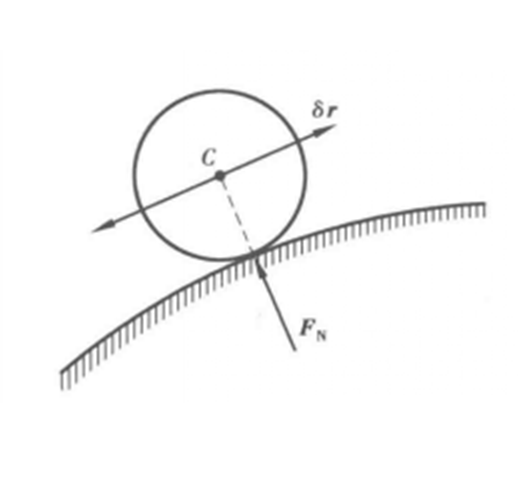 圖1 光滑接觸面約束
圖1 光滑接觸面約束無重剛桿約束
圖2所示為一無重剛性桿連線兩質點,A、B兩質點的約束反力 沿桿軸線,大小相等,方向相反。設A、B兩質點的虛位移分別為
沿桿軸線,大小相等,方向相反。設A、B兩質點的虛位移分別為 。由於質點系的虛位移應該滿足相容條件,剛性桿不能變形,A、B兩點的虛位移在AB連線上的投影必然相等,即有:
。由於質點系的虛位移應該滿足相容條件,剛性桿不能變形,A、B兩點的虛位移在AB連線上的投影必然相等,即有: 。因此,約束反力
。因此,約束反力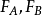 二力在相應的虛位移上的虛功之和為零。
二力在相應的虛位移上的虛功之和為零。



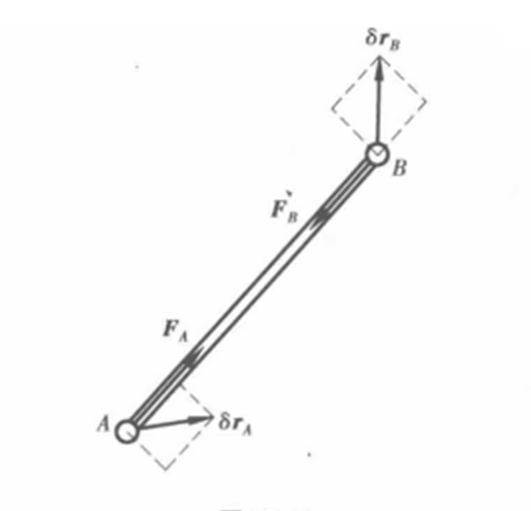 圖2 無重剛桿約束
圖2 無重剛桿約束連線兩剛體的光滑鉸鏈約束
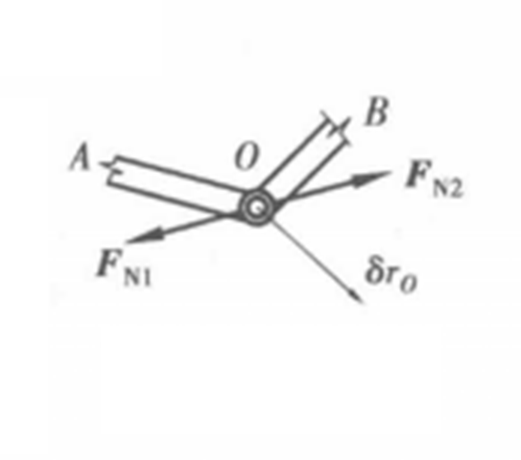 圖3 連線兩剛體的光滑鉸鏈約束
圖3 連線兩剛體的光滑鉸鏈約束不可伸長的繩索
圖4所示為一單擺,單擺由一端固定,另一端系住一質點M的不可伸長的繩索組成。設繩索不可伸長,小球在繩索的約束下,可在平面內擺動。將小球視為一個質點,如果在運動中,始終滿足約束條件,繩索既不鬆弛也不蜷曲,小球在鉛垂位置時,繩子給小球的約束力 (拉力),質點的虛位移必垂直於繩索拉力,為水平方向,拉力在該質點的虛位移的虛功等於零;當球擺到繩與鉛錘線成任意θ角時,繩子給小球的約束力,質點的虛位移沿小球軌跡的切線方向,仍然垂直於繩索拉力,即不可伸長的繩索拉力在質點的任何虛位移上的虛功等於零。
(拉力),質點的虛位移必垂直於繩索拉力,為水平方向,拉力在該質點的虛位移的虛功等於零;當球擺到繩與鉛錘線成任意θ角時,繩子給小球的約束力,質點的虛位移沿小球軌跡的切線方向,仍然垂直於繩索拉力,即不可伸長的繩索拉力在質點的任何虛位移上的虛功等於零。

 圖4 不可伸長的繩索
圖4 不可伸長的繩索無滑動的滾動
如圖5所示,圓輪在固定約束面上作無滑動的滾動,如果接觸面足夠剛性,可以略去滾動摩阻力偶,則當輪子作無滑動的滾動時,輪子與約束面的接觸點是輪子作平面運動的瞬心C,可以將輪子的運動看做是繞瞬心C作瞬時轉動,C點處的虛位移為零,約束輪子運動的法向力和摩擦力都通過C點,因此有: 。
。

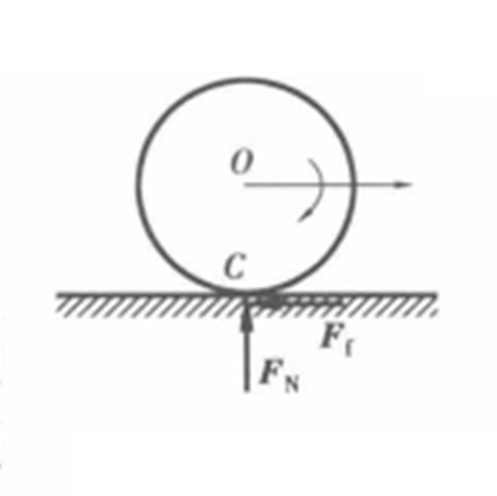 圖5 無滑動的滾動
圖5 無滑動的滾動



