在壓力容器的分析與計算中，往往忽略材料的強化作用，把材料看成一旦屈服就可以無限變形，這種材料模型稱理想彈塑性體。
基本介紹
- 中文名：理想彈塑性體
- 外文名：perfect elastic—plastic material
- 定義：材料一旦屈服就可以無限變形
- 公式：應力達到屈服點前服從虎克定律
- 特徵：安定定理
- 學科：材料力學
定義,彈塑性體的安定定理,靜力安定定理,機動安定定理,
定義
在壓力容器的分析與計算中，往往忽略材料的強化作用，把材料看成一旦屈服就可以無限變形，如圖1中A點為屈服點。這種材料模型稱理想彈塑性體(perfect elastic—plastic material)。這種材料，在應力達到屈服點以前完全服從虎克定律，屈服以後應力值不增加，應變值可無限增加。
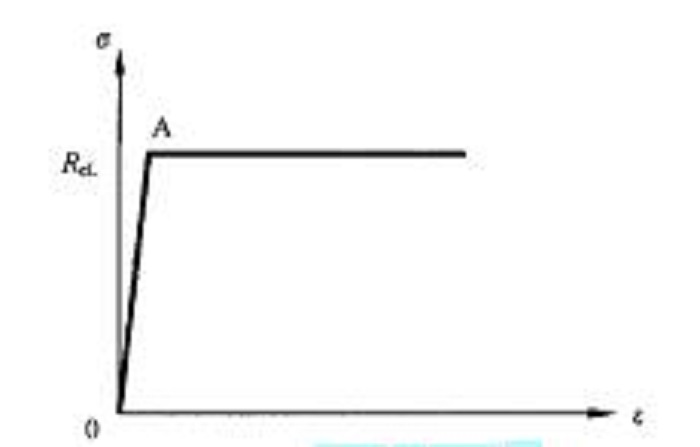圖1 理想彈塑性體彈塑性體的安定定理
如同極限分析，在對結構進行安定性分析時，往往不企圖對物體進行彈塑性分析，而是使用安定定理來找到所研究結構的安定載荷範圍的上限和下限。
安定(shakedown)一詞是著名塑性力學家W．Prager首先提出的，用來描述理想彈塑性體在反覆載荷作用下發生塑性變形之後的一種自適應特性。該詞的原意是指用瓶子裝糖或鹽時，經過數次晃動，可以裝得更多一些。在這裡當然是指物體經過一定量的塑性變形之後，產生了有利的殘餘應力場，使物體的彈性極限載荷有所提高。
這裡給出靜力安定定理(或下限安定定理，Melan，1938年)和機動安定定理(上限安定定理，Koiter，1956年)。
靜力安定定理
考慮理想彈塑性體，作用有體力Fi（x,t），面力Ti（x,t）以及在位移邊界上位移ui（x,t），如果在某一時刻以後能找到一個不依賴時間t的虛擬殘餘應力σij res（x）(它是一個自平衡應力場)。使得此後的完全彈性解σij e（x，t）在物體內處處滿足：
f (σij e+σij res)<0
即不違反屈服條件，則該物體是安定的。
安定性的形成就表示從某個循環載荷之後，物體不再產生塑性變形。對於理想彈塑性材料．外載荷所產生的應力與殘餘應力疊加後仍在屈服面內，即為彈性的。對於強化材料，由於強化規律的不同，其安定載荷的範圍也不同。
在利用Melan定理求解安定問題時，關鍵在於如何構造與時間無關的自平衡應力場，然後通過調整這些自平衡應力場參數，使載荷係數最大。
機動安定定理
考慮物體在循環載荷作用下的情形，對於作用有周期性變化的體力Fi(x,t)、面力Ti(x,t)和零位移邊界條件的理想剛塑性體，如果它是安定的，則對一切可能的機動容許的塑性應變率循環εij；在每個循環中其塑性耗散功不小於外載荷在ui res所作的功為
機動安定定理公式上式中σij是由εij通過正交流動法則求得的在屈服面上的應力。也就是說，如果上述的外力功大於結構內部的塑性耗散功，則結構不安定。
在利用Koiter定理求解安定問題時，需要建立機動容許的塑性應變率循環。其主要困難在於選取機動容許的塑性應變率場和處理時間積分。
