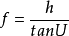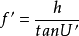基本特性
理想光學系統理論是在1841年由高斯提出來的,所以理想光學系統理論又稱為“高斯光學”。在各向同性的均勻介質中,理想光學系統的物像關係應具備以下特性:
1、點成點像:即對於物空間的每一點,在像空間必有一個點與之相對應,且只有一個點與之對應,這樣的兩個對應點稱為物像空間的
共軛點(如右圖中的A點和A′點)。
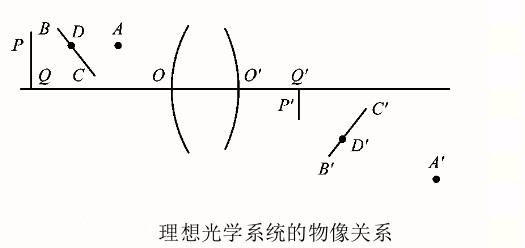
2、線成線像:即對於物空間的每一條直線,在像空間必有一條直線與之相對應,且只有一條直線與之對應,這樣的兩條對應直線稱為物像空間的共軛線(如右圖中的BC和B′C′)。
3、平面成平面像:即物空間的每一個平面,在像空間必有一個平面與之相對應,且只有一個平面與之對應,這樣的兩個對應平面稱為物像空間的共軛面(如右圖中的PQ面和P′Q′面)。
由此推廣,如果物空間上任意一點D位於直線BC上,那么其在像空間的共軛點D′也必位於共軛線B′C′上。同樣,物空間中的一個同心光束必對應於像空間中的另一同心光束。上述這種點對點、直線對直線、平面對平面的成像,稱為共線成像。
共線成像理論是理想光學系統的基礎理論,它只是基本假設,實際中是不存在這樣的理想光學系統的。顯然,理想光學系統是實際光學系統的努力方向,所以搞清楚理想光學系統的基本特徵,對尋求在某些方面接近於理想光學系統的實際系統是有益的。在設計實際光學系統時,人們常採用理想光學系統所抽象出來的一些光學特性和公式進行實際光學系統的初始計算,以使實際光學系統的設計成為可能,並使其計算得以簡化,質量得到提高。
在實際光學系統的近軸區可以滿足共線成像理論,因此,在進行光學系統設計時,往往以其近軸區的成像性質來衡量該系統的質量。
基點和基面
根據理想光學系統的特性,如果在物空間有一條和光學系統光軸平行的光線射入到理想光學系統,則在像空間必有一條光線與之相共軛。
如右圖所示,O
1和O
k兩點分別是理想光學系統第一面和最後一面的頂點,FO
1O
kF′為光軸。物空間的一條平行於光軸的直線AE
1經光學系統折射後,其折射光線G
kF′交光軸於F′點,另一條物方光線FO
1與光軸重合,其
折射光線O
kF′無折射地仍沿光軸方向射出。由於像方G
kF′、O
kF′分別與物方AE
1、FO
1相共軛,因此,交點F′為AE
1和FO
1交點(位於物方無窮遠的光軸上)的共軛點,所以F′是物方無窮遠軸上點的像,所有其它平行於光軸的入射光線均會聚於點F′,點F′稱為光學系統的像方焦點(或稱後焦點、第二焦點)。顯然,像方焦點是物方無限遠軸上點的共軛點。

同理,點F稱為光學系統的物方焦點(或稱前焦點、第一焦點),它與像方無窮遠軸上點相共軛。任意一條過F點的入射光線經理想光學系統折射後,出射光線必平行於光軸。通過像方焦點F′且垂直於光軸的平面,稱為像方焦平面(像方焦面);通過物方焦點F且垂直於光軸的平面,稱為物方焦平面(物方焦面)。顯然,像方焦平面的共軛面在無窮遠處,像方焦平面上任何一個物點發出的光束,經理想光學系統出射後必為一平行光束;同樣,物方焦平面的共軛面也在無窮遠處,任何一束入射的平行光,經理想光學系統折射後,必會聚於像方焦平面上的某一點。必須指出,焦點和焦面是理想光學系統的一對特殊的點和面。物方焦點F和像方焦點F′彼此之間不共軛,同樣,物方焦平面和像方焦平面也不共軛。
如右圖所示,延長入射光線AE
1和出射光線G
kF′,得到交點Q′;同樣,延長入射光線BE
k和G
1F,可得交點Q。設光線AE
1和BE
k的入射高度相同,且都在子午面內。顯然點Q和點Q′是一對共軛點。點Q是光線AE
1和FQ交成的“虛物點”;點Q′是光線BE
k和G
kF′交成的“虛像點”。過點Q和點Q′作垂直於光軸的平面QH和Q′H′,則這兩個平面亦相互共軛。由圖可知,位於這兩個平面內的共軛線段QH和Q′H′具有相同的高度,且位於光軸的同一側,故其垂軸放大率β =+1。我們稱垂軸放大率為+1的這一對共軛面為主平面,其中的QH稱為物方主平面(或前主面、第一主面),Q′H′稱為像方主平面(或後主面、第二主面)。物方主平面QH與光軸的交點H稱為物方主點,像方主平面Q′H′與光軸的交點H′稱為像方主點。

主點和主平面也是理想光學系統的一對特殊的點和面。物方主平面和像方主平面、物方主點和像方主點,它們彼此之間是共軛的。
自物方主點H到物方焦點F的距離稱為物方焦距(或前焦距、第一焦距),用f表示;自像方主點H′到像方焦點F′的距離稱為像方焦距(或後焦距、第二焦距),用f′表示。焦距的正、負是以相應的主點為原點來確定的。若由主點到相應焦點的方向與光線傳播方向相同,則焦距為正;反之為負。圖上中所示的情況為f<0,f′>0。
由△FQH和△F′Q′H′得到物方焦距和像方焦距的表達式為
一對主點和一對焦點構成了光學系統的基點,一對主面和一對焦面構成了光學系統的基面,它們構成了一個光學系統的基本模(如右圖所示)型。對於理想光學系統,不管其結構(r,d,n)如何,只要知道其焦距值和焦點或主點的位置,其性質就確定了。

物像關係式
已知一理想光學系統的基點、基面位置,當物體的位置和大小一定時,即可用解析法求出像的位置和大小。為了導出有關的物像位置公式,先要確定物像的有關參數。
牛頓公式
如右圖,大小為y的物體AB經理想光學系統後,其像A′B′的大小為y′。系統中F、F′、H、H′的位置均為已知。

牛頓公式中物體AB的物距x是以物方焦點F為原點,物距x的正負號按以下規則判定:若由物方焦點F到物點A的方向與光線傳播方向一致,則物距x為正;反之為負。圖中的物距x為負。同樣,像距x′是以像方焦點F′為原點至像點A′,若與光線的傳播方向一致,則像距為正,反之為負。圖中的像距x′為正。
由相似△BAF和△RHF可得
同樣,在△Q′H′F′和△B′A′F′中有
由此可得
這就是以焦點為原點的物像位置公式,稱為牛頓公式。
高斯公式
高斯公式的物像位置是相對於理想光學系統的主點來確定的。如上圖所示,以
表示物點A到物方主點H的距離,以
表示像點A′到像方主點H′的距離。方向規定以主點為原點,如果由H到A或由H′到A′的方向與光線的傳播方向一致,則為正;反之為負。由圖可得
代入牛頓公式整理得
這就是以主點為原點的物像位置公式,稱為高斯公式。